Espaces préhilbertiens
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
 par legeniedesalpages » 19 Fév 2008, 16:26
par legeniedesalpages » 19 Fév 2008, 16:26
Bonjour,
je ne vois pas comment résoudre cet exercice:
Soit
)
un

-espace préhilbertien de

-produit scalaire associé
)
.
On suppose qu'il existe un réel

tel que pour tous
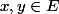
on ait:
[CENTER]
| = \gamma ||x||. ||y||)
[/CENTER]
Montrer que

est soit l'espace vectoriel nul, soit de

-dimension 1.
Je ne vois pas vraiment comment commencer cet exo.
Merci pour vos indications.
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 19 Fév 2008, 16:47
par Skullkid » 19 Fév 2008, 16:47
Bonjour, sauf erreur de ma part, ça marche en supposant par l'absurde que E est au moins de dimension 2. On peut alors prendre deux vecteurs unitaires orthogonaux dans E.
(J'ai jamais travaillé sur des préhilbertiens sur

différent de

ou

mais je suppose que ça fonctionne à peu près de la même façon...pardon d'avance si je me suis trompé)
 par legeniedesalpages » 19 Fév 2008, 16:56
par legeniedesalpages » 19 Fév 2008, 16:56
Bon je crois que j'ai trouvé en fait:
On suppose que

.
si
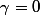
, on a
[CENTER]
| = 0)
quelque soit

, [/CENTER]
ce qui est absurde car
)
est définie positive.
Donc

.
Soient
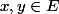
et supposons que quelque soit
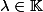
, on a

.
On a
[CENTER]
| = \gamma ||x-\lambda y||^2)
, [/CENTER]
ceci n'est possible que si

,
autrement dit

.
Donc

et

sont colinéaires, D'où

est de dimension 1. Mais c'est bizarre j'ai l'impression que du coup pour n'importe quel
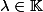
, on a

? :briques:
 par legeniedesalpages » 19 Fév 2008, 17:04
par legeniedesalpages » 19 Fév 2008, 17:04
pardon, je viens de réaliser que j'ai dit n'importe quoi, je rédige.
 par legeniedesalpages » 19 Fév 2008, 17:13
par legeniedesalpages » 19 Fév 2008, 17:13
On suppose que

.
si
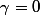
, on a
[CENTER]
| = 0)
quelque soit

, [/CENTER]
ce qui est absurde car
)
est définie positive.
Donc

.
Soient
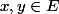
et supposons que quelque soit
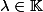
, on a

.
On a
[CENTER]
| = \gamma ||x-\lambda y||^2)
, [/CENTER]
si

, ceci n'est possible que si

, autrement dit

, ce qui est contradictoire.
Donc

.
L'égalité qu'on dispose dans les hypothèses devient alors:
[CENTER]
| = ||x||.||y||)
,[/CENTER]
qui a lieu seulement lorsque

et

sont collinéaires, ce qui est de nouveau contradictoire.
Donc

et

sont colinéaires.
En laissant fixe un vecteur

non nul et en parcourant

par

, on en déduit alors que

est de dimension 1.
 par legeniedesalpages » 19 Fév 2008, 17:27
par legeniedesalpages » 19 Fév 2008, 17:27
suite à ta remarque Skullid,
déjà on peut dire qu'on l'a montré pour la cas où

est de caractéristique 0, sans cette hypothèse je me demande si ça reste vrai. :hein:
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 19 Fév 2008, 17:41
par Skullkid » 19 Fév 2008, 17:41
A en croire Wikipedia, un espace préhilbertien est par définition réel ou complexe, donc y a pas de problème de caractéristique. Y a une définition plus générale dans ton cours ?
Dans ma démonstration, je supposais que E était au moins de dimension 2 et je considérais

deux vecteurs unitaires orthogonaux. Alors
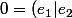=\gamma ||e_1||.||e_2||=\gamma)
, d'où une contradiction.
 par legeniedesalpages » 19 Fév 2008, 17:54
par legeniedesalpages » 19 Fév 2008, 17:54
Skullkid a écrit:A en croire Wikipedia, un espace préhilbertien est par définition réel ou complexe, donc y a pas de problème de caractéristique. Y a une définition plus générale dans ton cours ?
Dans ma démonstration, je supposais que E était au moins de dimension 2 et je considérais

deux vecteurs unitaires orthogonaux. Alors
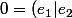=\gamma ||e_1||.||e_2||=\gamma)
, d'où une contradiction.
Non dans mon cours il n'y a aucune précision sur

, mis à part le fait que c'est un corps.
Mais comment on voit que dans un espace de dimension
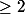
, on dispose d'au moins deux vecteurs unitaires orthogonaux? et comment sait-on que deux vecteurs orthogonaux sont libres?
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 19 Fév 2008, 18:22
par Skullkid » 19 Fév 2008, 18:22
Si on a une famille libre
)
on peut l'orthonormaliser par Schmidt :

et

avec
e_1)
.
Mais je crois que forcément
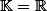
ou

puisqu'une norme est à valeurs dans

et que le produit scalaire est à valeurs dans

.
(En gros je crois qu'on se prend la tête pour rien xD)
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 19 Fév 2008, 18:47
par ThSQ » 19 Fév 2008, 18:47
legeniedesalpages a écrit:[CENTER]
| = \gamma ||x||. ||y||)
[/CENTER]
Ca veut dire que l'angle est constant entre deux vecteurs. Si la dim est > 1 on peut toujours construire deux vecteurs orthogonaux non nuls.
Edit : c'est l'idée de skullkid d'ailleurs ..
 par legeniedesalpages » 19 Fév 2008, 21:02
par legeniedesalpages » 19 Fév 2008, 21:02
Skullkid a écrit:Si on a une famille libre
)
on peut l'orthonormaliser par Schmidt :

et

avec
e_1)
.
je ne vois pas pourquoi
=0)
?
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 19 Fév 2008, 21:29
par Skullkid » 19 Fév 2008, 21:29
=\frac{1}{||v_2||}(e_1|v_2)=\frac{1}{||v_2||}[(e_1|x_2)-(e_1|x_2)(e_1|e_1)]=0)
car

 par legeniedesalpages » 25 Fév 2008, 18:50
par legeniedesalpages » 25 Fév 2008, 18:50
Skullkid a écrit:=\frac{1}{||v_2||}(e_1|v_2)=\frac{1}{||v_2||}[(e_1|x_2)-(e_1|x_2)(e_1|e_1)]=0)
car

ah oui effectivement,
merci SkullId.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 43 invités
deux vecteurs unitaires orthogonaux. Alors
, d'où une contradiction.