Espaces de Banach
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
 par legeniedesalpages » 05 Mai 2008, 00:32
par legeniedesalpages » 05 Mai 2008, 00:32
Bonsoir,
je bloque sur cet exercice:
Soit

un espace de Banach Et
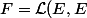)
, l'espace de Banach des applications linéaires continues de

dans

. On munit

de la norme d'opérateur induite par la norme de

.
1) Montrer que si

et

sont dans

,
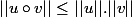
.
2) Montrer que, si
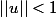
, la série
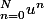
converge dans

. En déterminer la limite.
3) Montrer que
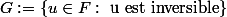
est un ouvert de

.
Pour la 1) c'est ok, après pour la 2) je ne vois pas comment déterminer la limite. Pour la 3) je ne vois pas comment attaquer. :hein:
Merci pour votre aide.
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 05 Mai 2008, 00:47
par ffpower » 05 Mai 2008, 00:47
Indic:se servir de la question 2 lol.Si u est inversible et v de norme petite alors u+v=u(id+vu^(-1)) or id+uv^(-1) est....Je te laisse compléter
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 05 Mai 2008, 02:39
par barbu23 » 05 Mai 2008, 02:39
Ben pour
 $)
tu considères l'ensembles des endomorphismes à determinant non nul et le determinant est une application continue n'est ce pas ? et

est exactement le noyaux de ce detrminant ... etc ... et tu deduis le resultat !!
Pour
 $)
ben il faut retourner à mon avis au cors sur les series entières ...
regarde ici :
http://c.caignaert.free.fr/chapitre11/node1.htmlBonne chance ... !
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 05 Mai 2008, 02:44
par barbu23 » 05 Mai 2008, 02:44
parceque à mon avis, ta serie s'ecrit comme ça :
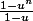
( suite ) ... ben etudie la convergence de cette suite là ... ! n'est ce pas ... ?
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 05 Mai 2008, 07:21
par ffpower » 05 Mai 2008, 07:21
Le déterminant dans un Banach? :hum:
 par legeniedesalpages » 05 Mai 2008, 10:51
par legeniedesalpages » 05 Mai 2008, 10:51
Merci pour vos réponses.
Pour la 2), je crois que j'ai compris:
Pour tout entier

, on note
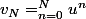
.
On a
 = \textrm{Id}_E-u^{N+1})
,
or
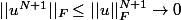
quand
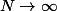
car
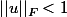
.
Donc
\rightarrow \textrm{Id}_E)
quand
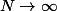
.
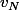
tend vers un vecteur

quand
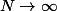
relativement à le norme
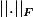
et l'application
\rightarrow f\circ g)
de
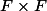
dans

est continue.
Donc
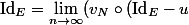) = (\lim_{n\rightarrow \infty} v_N)\circ (\textrm{Id}_E-u) = v\circ (\textrm{Id}_E-u))
.
On montre de même que
\circ v = \textrm{Id}_E)
, ainsi
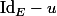
est inversible dans

et
^{-1}=\Bigsum_{n=0}^{\infty}u^n)
.
Je regarde pour la 3)

 par legeniedesalpages » 05 Mai 2008, 11:19
par legeniedesalpages » 05 Mai 2008, 11:19
ffpower a écrit:Indic:se servir de la question 2 lol.Si u est inversible et v de norme petite alors u+v=u(id+vu^(-1)) or id+uv^(-1) est....Je te laisse compléter
là je ne comprends pas. :hein:
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 05 Mai 2008, 11:54
par ffpower » 05 Mai 2008, 11:54
On a u+v=u(id+vu^(-1)).On sait que u est inversible,il reste a voir si id+vu^(-1) est inversible lui aussi.Si on pose w=-vu^(-1),alors id+vu^(-1)=id-w
Or d apres la question 2...
 par legeniedesalpages » 05 Mai 2008, 12:19
par legeniedesalpages » 05 Mai 2008, 12:19
ffpower a écrit:On a u+v=u(id+vu^(-1)).On sait que u est inversible,il reste a voir si id+vu^(-1) est inversible lui aussi.Si on pose w=-vu^(-1),alors id+vu^(-1)=id-w
Or d apres la question 2...
ah oui, merci, donc d'après la question 2)
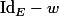
est inversible dès que
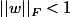
, ie
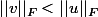
,
mais en quoi ça montre que

est intérieur à

?
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 05 Mai 2008, 12:40
par ffpower » 05 Mai 2008, 12:40
Et bien on a montrer que si v est de norme assez petite,u+v est dans G.C est précisément la définition de u interieur a G:Ya une boule centrée en u incluse dans G..
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 05 Mai 2008, 15:27
par barbu23 » 05 Mai 2008, 15:27
bonjour :
J'ai pas trop compris le principe pour montrer que la serie de legeniealpagesconverge dans

...
merci d'avance !!
 par legeniedesalpages » 05 Mai 2008, 15:40
par legeniedesalpages » 05 Mai 2008, 15:40
barbu23 a écrit:bonjour :
J'ai pas trop compris le principe pour montrer que la serie de legeniealpagesconverge dans

...
merci d'avance !!
Salut, ben c'est ton principe lol:
barbu23 a écrit:parceque à mon avis, ta serie s'ecrit comme ça :
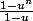
( suite ) ... ben etudie la convergence de cette suite là ... ! n'est ce pas ... ?
sauf que l'écriture

n'a pas de sens pour les endomorphismes (division non définie), donc on a plutôt
\circ (\Bigsum_{n=0}^N u^n)= (\Bigsum_{n=0}^N u^n) \circ (1_F-u)=1_F-u^{N+1})
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 05 Mai 2008, 16:02
par barbu23 » 05 Mai 2008, 16:02
Ah oui, t'as parfaitement raison ... ! :dodo: :doh:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 57 invités
...
( suite ) ... ben etudie la convergence de cette suite là ... ! n'est ce pas ... ?