Salut,
C'est élémentaire à condition de savoir que

désigne le dual
topologique (et pas algébrique) de l'espace vectoriel normé

, c'est à dire l'ensemble des applications linéaires
continues (et pas l'ensemble de toutes les applications linéaires).
Bref, ta fonction

est continue et ça signifie qu'il existe uen consytante

telle que, pour tout

on ait
|\!\leq\!M\|x\|_\infty)
(et le plus petit tel

, c'est, par définition, la norme de

).
Ensuite, si tu considère un entier naturel

quelcoqnque et que tu considère la suite
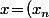_{n\geq})
définie par
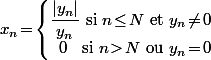
alors on a clairement

et

donc
|\!\leq\!M)
.
Sauf que, vu la construction de

, on a
|\!=\!\sum_{n=0}^N|y_n|)
donc en fait

et comme cete inégalité est vrai pour tout entier

(et que

ne dépend pas de

) ça prouve la convergence de

et ça prouve même que la série converge vers une réel
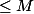
donc que

vu qu'on peut prendre