Tu fais bien de te poser des questions!
C'est le théorème de la base incomplète, il utilise l'axiome du choix qui est encore un axiome "contesté" par certains mathématiciens (mais accepté par la quasi totalité)
https://fr.wikipedia.org/wiki/Th%C3%A9o ... pl%C3%A8tehttps://fr.wikipedia.org/wiki/Axiome_du_choixCa te donne l'existence d'une base pour ton EV mais certainement pas la gueule qu'il a !
Par contre pour aller plus loin, des espaces pas si différents dans l'esprit (les fonctions continues sur [0,2pi] ou sur autre intervalle), il me semble que l'on peut
presque écrire que
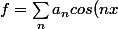 + b_n sin(nx))
Avec

et

les coefficients de Fourier de f
Après f est somme d'une infinité de termes, c'est pas une base (pour une base
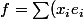)
avec
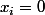
à partir d'un certain rang) mais c'est ce qu'on appelle base hilbertienne
L'égalité est pas vraiment vraie pour tout x, je suis pas très rigoureux y a des hypothèses quand même supplémentaires dont je me rappelle plus pour tout te dire mais ut vois l'esprit
