Espace vectoriel sur un sous-corps réel.

[Nightmare]

Salut à tous :happy3:

Je ne sais pas si le problème suivant a déjà été posté, mais je le trouve très intéressant et pas facile.

Le problème tient en une phrase :

Peut-on trouver un sous-corps k de tel que soit un k-espace vectoriel de dimension finie?

Bon courage :happy3:

[nuage]

Salut,
il est évident que convient.
je ne crois pas qu'il y en ai d'autres, mais je peut me tromper.
Ma croyance est basée sur le fait qu'un tel sous-corps contient tous les éléments transcendants de comme sur-corps de .

[Nightmare]

Pas d'idées? :happy3:

[yos]

C'est un problème compliqué. Je crois me souvenir que la réponse est non. J'avais trouvé les outils nécessaire dans le livre de Malliavin "algèbre commutative".

[Nightmare]

Ce ne doit pas être le même problème. La réponse est oui !

[nuage]

Ce ne doit pas être le même problème. La réponse est oui !

Car R est un ev de dimension finie sur R.
On a donc au moins un exemple.

[yos]

Oui ou non je sais plus trop, mais je doute que tu puisses apporter une réponse simple à ce truc.

[SimonB]

Je cherche des arguments probants (dénombrabilité, théorie des corps...) mais je ne trouve pas.
Je veux bien qu'on me guide :)

[Nightmare]

la solution que je connais est de la théorie de Galois pure :happy3:

[Doraki]

J'ai un lemme qui dit que si on a un sous-corps K de R et un x tels que R = K(x) alors comme sqrt(|x|) est dans R = K(x), x et R sont algébriques sur K, et donc que dim_K(R) est finie.

Reste à montrer qu'il existe K et x tels que R = K(x), ce qui ne me paraît pas moins impossible a priori.

[Nightmare]

C'est une idée intéressante. Ce théorème est vrai, la démonstration est quasiment la même que l'existence d'une base dans un ev. On remarque d'ailleurs (et on s'en doutait) qu'on a besoin de l'axiome du choix !

[yos]

Inversement :
si un sous-corps K de R est tel que l'extension R/K est finie, alors quitte à remplacer K par un corps intermédiaire, tu as R=K(x) pour un certain x.
Et biensûr R/K algébrique.
Il faut donc fourrer dans K une base de transcendance.

[ffpower]

Je m étais posé moi aussi de mon coté cette question:peut on ecrire R=k(x) avec k différent de R.J y avais pas mal réfléchi et m'étais entre autre ramené a cette equivalance que vous venez d etablir,mais je n ai pas reussi a conclure.Le mieux que j ai obtenu,c est l existence d un sous corps strict k tel que tout reel est algebrique sur k.C est pourquoi j attend ta solution avec impatiance^^

[Nightmare]

Je laisse chercher un peu je posterai si personne ne trouve :happy3:

[yos]

la solution que je connais est de la théorie de Galois pure

Pour R/K galoisienne, en tout cas, je peux te dire qu'il y en a pas.

[ffpower]

oui car sinon y aurait des auto non triviaux de R,j ai eu ca aussi :we:

[SimonB]

Nightmare pourrait-il nous éclairer ?

[Nightmare]

Salut à tous :happy3:

Une idée est de considérer l'ensemble des extentions de Q qui ne contiennent pas . Cet ensemble inductif admet un élément maximal. Voir ce qu'on peut faire avec ce dernier :happy3:

[yos]

J'avais essayé des constructions comme ça.
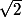
Si on n'y met pas , on doit pas y mettre ni ...
A la fin ça fait du monde entre ton élément maximal K et le corps R. pour la dimension finie c'est pas gagné.

[Nightmare]

Effecitvement, ce n'est pas K qui convient. Par contre si on considère K(x) où x est transcendant sur Q...