Espace vectoriel sur un sous-corps réel.
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 08 Juin 2009, 16:56
par yos » 08 Juin 2009, 16:56
Nightmare a écrit:l'ensemble des extentions de Q qui ne contiennent pas

. Cet ensemble inductif
Pourquoi inductif?
)
et
)
sont éligibles mais pas le corps composé des deux.

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 08 Juin 2009, 18:20
par leon1789 » 08 Juin 2009, 18:20
yos a écrit:J'avais essayé des constructions comme ça.
Si on n'y met pas
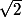
, on doit pas y mettre

ni

...
A la fin ça fait du monde entre ton élément maximal K et le corps R. pour la dimension finie c'est pas gagné.
C'est pourtant ce qui se passe pour C/R : on enlève les racines de -1, et ses propres racines, etc... et pourtant on reste en dimension 2.

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 08 Juin 2009, 18:25
par leon1789 » 08 Juin 2009, 18:25
yos a écrit:Pourquoi inductif?
)
et
)
sont éligibles mais pas le corps composé des deux.
Un ensemble partiellement ordonné (ici, les sous-corps de R) est inductif si toute partie totalement ordonnée (typiquement une famille de sous-corps
comparables) admet un majorant (la réunion de tous les sous-corps de cette famille).
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 08 Juin 2009, 18:59
par yos » 08 Juin 2009, 18:59
leon1789 a écrit:C'est pourtant ce qui se passe pour C/R : on enlève les racines de -1, et ses propres racines, etc... et pourtant on reste en dimension 2.
Oui c'est vrai : la dimension peut rester finie.
leon1789 a écrit:Un ensemble partiellement ordonné est inductif si toute partie totalement ordonnée admet un majorant
En effet : je connais pas mes définitions.
Reste à voir ce qu'on peut faire avec ce K(x) dont parle Nightmare : j'y penserai.
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 08 Juin 2009, 19:49
par ffpower » 08 Juin 2009, 19:49
c etrange que K ne convienne pas et K(x) si.en effet,x est algebrique sur K,donc K(x) est juste une extension finie de K..
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 09 Juin 2009, 12:40
par yos » 09 Juin 2009, 12:40
Il faut prendre x hors de K sinon on n'avance pas. Un tel x existe-t-il? Seul R contient tous les transcendants et

donc ça doit marcher
K(x) contient
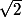
par maximalité de K.
\subset R)

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 09 Juin 2009, 20:50
par leon1789 » 09 Juin 2009, 20:50
yos a écrit:Il faut prendre x hors de K sinon on n'avance pas. Un tel x existe-til?
Soit x transcendant sur Q. Si x appartient à K, alors

(transcendant sur Q également) n'appartient pas à K. Quitte à changer

en x, on peut effectivement supposer que K ne contient pas x.
yos a écrit:K(x) doit contenir
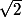
par maximalité de K.
\subset K(x)\subset R)
.
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 09 Juin 2009, 21:16
par yos » 09 Juin 2009, 21:16
yos a écrit: Un tel x existe-t-il? Seul R contient tous les transcendants et

donc ça doit marcher
J'avais répondu à ma propre question mais c'est pas grave.

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 09 Juin 2009, 21:23
par leon1789 » 09 Juin 2009, 21:23
yos a écrit:J'avais répondu à ma propre question mais c'est pas grave.
oui, mais qu'entends-tu par > ?

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 09 Juin 2009, 21:31
par leon1789 » 09 Juin 2009, 21:31
yos a écrit:Seul R contient tous les transcendants
Pourquoi n'existe-t-il pas un sous-corps réel E tel que
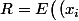_{i\in I} \,\big))
où tous les

sont algébriques sur Q ?
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 10 Juin 2009, 17:02
par ffpower » 10 Juin 2009, 17:02
peut on avoir la soluce?je cale :marteau:
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 10 Juin 2009, 18:18
par yos » 10 Juin 2009, 18:18
Il y a un théorème d'Artin qui dit que si la cloture algébrique
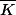
d'un corps K est de degré fini sur K, alors

. Je vais regarder si je comprend la preuve.
En tout cas, voilà de quoi abandonner tout espoir.
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 10 Juin 2009, 19:47
par ffpower » 10 Juin 2009, 19:47
wow,c gros ca...et du coup,c est mal barré ouai
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 11 Juin 2009, 18:41
par yos » 11 Juin 2009, 18:41
http://www-fourier.ujf-grenoble.fr/enseignement/IMG/pdf/TERsujets09.pdfVoici une référence pour ceux qui douteraient : Nightmare s'est donc planté ou a de mauvaises sources.
Le théorème d'Artin-Schreier que j'ai cité plus haut est pas très dur à prouver en fait. Il nécessite le cas simple de la théorie de Kummer (caractérisation des extensions
)
lorsque K contient les racines n-ème de 1). Il y a aussi un autre point technique qui me semble contournable en caractéristique 0 (notre cas). On trouve ça dans les bouquins suivants :
- Ribenboïm, l'arithmétique des corps;
- Bourbaki, algèbre, ch. V, exercice 11.
-
SimonB
 par SimonB » 12 Juin 2009, 08:15
par SimonB » 12 Juin 2009, 08:15
J'aimerais quand même bien voir Nightmare revenir par ici pour nous dire ce qu'il en pense ! :)
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 12 Juin 2009, 11:52
par Nightmare » 12 Juin 2009, 11:52
SimonB a écrit:J'aimerais quand même bien voir Nightmare revenir par ici pour nous dire ce qu'il en pense !

Salut à tous :happy3:
Effectivement après relecture de vos posts ma preuve n'est pas bonne ! L'extension qu'on obtient est de dimension dénombrable mais pas finie ...
Bon, si on appelle K un tel corps. Considérons l'extension
\subset \mathbb{C})
. Elle est finie et galoisienne donc il existe un sur-corps K' de K(i) strictement contenu dans
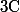
et tel que
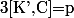
premier
On montre que K' contient toutes les racines p-ème de l'unité et que comme le signal Yos on en déduit que
)
avec x dans K'.
Le polynôme minimal

de

est irréductible dans

et si p est différent de 2, on montre qu'il y a contradiction avec le caractère algébriquement clos de
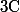
puisque

serait irréductible.
Finalement p=2.
Mes calculs mènent alors à
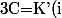)
ce qui amène à une autre contradiction.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 28 invités
. Cet ensemble inductif
, on doit pas y mettre
ni
...
et
sont éligibles mais pas le corps composé des deux.
par maximalité de K.
.