Espace vectoriel et sous groupe
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Pythix
- Membre Relatif
- Messages: 134
- Enregistré le: 26 Oct 2005, 13:42
-
par Pythix » 25 Mai 2008, 10:16
Bonjour,
je bloque sur cet exercice :
soient E un K-espace vectoriel de dimension finie et F un sous espace vectoriel de L(E) contenant id et stable par o.
Montrer que
)
est un sous groupe de GL(E).
J'ai essayé de partir sur la caractérisation classique d'un sous groupe, mais difficile de montrer de montrer la stabilité par o et que l'inverse est dans F...
Si quelqu'un a une idée... Merci d'avance
-
Clembou
- Membre Complexe
- Messages: 2732
- Enregistré le: 03 Aoû 2006, 11:00
-
par Clembou » 25 Mai 2008, 10:21
Pythix a écrit:Bonjour,
je bloque sur cet exercice :
soient E un K-espace vectoriel de dimension finie et F un sous espace vectoriel de L(E) contenant id et stable par o.
Montrer que
est un sous groupe de GL(E).
J'ai essayé de partir sur la caractérisation classique d'un sous groupe, mais difficile de montrer de montrer la stabilité par o et que l'inverse est dans F...
Si quelqu'un a une idée... Merci d'avance
Rappelles moi : GL(E), c'est bien tous les éléments inversibles de E... or
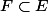
. Donc
 \subset E)
, en particulier
 \subset GL(E))
donc tu peux déjà en déduire l'inverse de
)
est dans
)
.
-
kazeriahm
- Membre Irrationnel
- Messages: 1608
- Enregistré le: 04 Juin 2006, 09:49
-
par kazeriahm » 25 Mai 2008, 12:45
bah la sabilité par ° c evident etant donné que F est lui meme stable par ° par hypothèse
pour montrer que F est stable par passage à l'inverse :
soit f un endomorphisme inversible de F.
Considère l'application qui à toute fonction g de F inter GL(E) associe g°f. Que peux tu dire de cette application ? Que peux tu en conclure etant donné que E est de dimension finie ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 17 invités
