Espace vectoriel et sous-espaces vectoriels, combinaisonslin

[meysan]

Bonjour,

J'ai beaucoup de mal à faire l'exercice suivant car je n'arrive pas définir l'ensemble S pour prouver qu'il s'agit d'un sous-espace vectoriel.

Voici l'énoncé:

On appelle support d'une suite () l'ensemble .

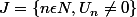
Montrer que l'ensemble S des suites réelles à support fini est un espace vectoriel pour les lois usuelles.

Merci à vous

[Rdvn]

Bonsoir
Considérons E, l'ensemble des suites réelles.
E est muni d'une structure d'espace vectoriel pour les lois + et . habituelles .
S est un sous-ensemble, non vide, de E
(S contient la suite nulle, entre autres)
Reste à montrer la stabilité de S pour les deux lois, ce qui n'est pas très compliqué)
Bon courage