Espace vectoriel normé

[stansoad0108]

Bonjour à tous,

Voila je bloque sur un exercice, qui est pour moi, difficile à comprendre...si vous pouvez m'éclaircir, m'indiquer quelques pistes pour démarrer...ca serait gentil

Code: Tout sélectionner

Soit (E, ||.||) un espace vectoriel normé de dimension finie.

Montrer que tout sous-espace vectoriel F de E est fermé dans E.
Montrer que E est le seul sous-espace vectoriel de E qui soit ouvert.

Merci ++

[Skullkid]

Bonsoir,

1 - Comment peut-on montrer qu'un ensemble est fermé ?
2 - Essaye de voir ce que donnerait un sev strict de E qui serait ouvert.

Dans les deux cas, pense à utiliser l'hypothèse de dimension finie.

[ThSQ]

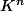
Le 1 se généralise : tout sev de dim finie est fermé (que l'espace le soit ou pas) : "c'est" qui est complet (K = R ou C de préférence sinon c'est un peu faux).

Le 2 se généralise aussi à tout evn. Le seul sev ouvert = espace total. Une boule ouvert est isotrope, elle permet d'atteindre par homothétie tout l'espace.