Bonjour
Du point de vue notation, si on veut respecter l'énoncé les indices des composantes sont en bas. Donc perso c'est ce que je vais faire.
D'abord pour faire simple considérons l'opérateur de

de
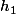
vers
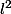
définie par
=(n a_n)_n.)

est bien défini puisque
||_{l^2}^2=\sum_n n^2 |a_n|^2\leq ||a||_{h_1}^2.)
De plus remarquons que
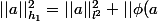||_{l^2}^2.)
Alors si
})_n)
est une suite de Cauchy dans
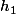 ,
, c'est équivalent à dire que
})_n)
est une suite de Cauchy dans
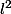
ainsi que
})_n).)
On en déduite que la suite
})_n)
converge vers une suite

dans
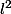
et
})_n))
vers une suite b dans

Maintenant c'est clair que si une suite converge dans

chaque composante de la suite converge vers chaque composante correspondante de la limite.
C'est pourquoi on a pour chaque composante d'indice k:
}})
converge vers

et

converge vers

On en tire donc que
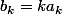
, pour tout k. Donc que
)
et que
})_n)
converge vers a dans

c.q.f.d
La deuxième question est évidente.

