Espace réflexif suite bornée et convergence faible

[melreg]

Bonjour,

Dans mon cours d'analyse fonctionnelle, j'ai le théorème suivant

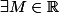
Soit H un espace de Hilbert séparable et une suite bornée de H (i.e. t.q.). Alors il existe une sous-suite de qui converge faiblement vers un élément x de H.

Après ce théorème, j'ai une remarque qui dit que ce théorème reste vrai pour un espace de Banach réflexif. Mais cette fois il n'y a pas de preuve.
Est-ce que quelqu'un a une idée de comment se déroule la preuve?

Merci d'avance

[Nightmare]

Salut :happy3:

Il te suffit de montrer que la boule unité est compact. Par réflexivité, il suffit de montrer que la boule unité de son espace dual est elle-même compact.

Pour cela, on identifie le dual à l'espace produit . la boule unité fermé de cet espace est contenue dans le produit des boules centrée en l'origine de rayon ||x|| avec x décrivant l'espace de départ. Par le théorème de Tychonov, on a la compacité du produit et par fermeture de la boule unité, on a la compacité de cette dernière.

:happy3:

[melreg]

Waouw, tu es calé sur le sujet!!! Je regarde tout ça tranquillement de mon côté...
Merci!

[Nightmare]

J'ai oublié de préciser mais ça va de soi : La compacité est relative à la topologie faible. Lorsqu'on identifie le dual à l'espace produit, on passe bien sûr à la topologie produit induite.

[ThSQ]

Il te suffit de montrer que la boule unité est compact. Par réflexivité, il suffit de montrer que la boule unité de son espace dual est elle-même compact.

Bidual plutôt non ? (mais ça change rien à la suite)

[Nightmare]

Pourquoi Bidual ?

[ThSQ]

Ben réflexif c'est isométrique au bidual pas au dual

[Nightmare]

Ok, on parlait pas du même espace de départ.

Je parlais du dual de E* donc effectivement du bidual.

[ThSQ]

Ben tu disais "son espace dual" mais bon bref, c'est pas grave :++: