Bonjour,
Soient

et

deux espaces topologiques quelconques et

une application telle que :
 = f(x_2 ) $)
.
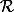
est une relation d'équivalence.

induit une application :

telle que :

avec :

.
1 ) Montrer que l'ensemble des parties

telles que
 $)
est un ouvert de

est une topologie sur

vérifiant la propriété universelle suivante :

est continue si et seulement si

est continue.
2 ) Montrer qu'un topologie sur

vérifiant la propriété universelle précédente est nécessairement celle introduite dans la question 1 ).
Voici ce que j'ai fait :
1 ) On pose :
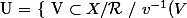 \text{ est un ouvert de} \ X \} $)
Montrons que

est une topologie.
-
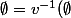 $)
est un ouvert de

, donc


car
 = X $)
est un ouvert de

.
- Soient

, alors :
 $)
et
 $)
sont deux ouvert de

Par conséquent :
 = v^{-1} ( V_1 ) \bigcap v^{-1} ( V_2 ) $)
est un ouvert de

.
donc :

- Soient
_{i \in I} \subset U $)
, alors :
 $)
est un ouvert de

.
Par conséquent :
 = \displaystyle \bigcup_{i \in I} v^{-1} ( V_i ) $)
est un ouvert de

.
Donc :

Par conséquent :

est une topologie sur

Soit

est continue


un ouvert de

:
 $)
est un ouvert de


 = ( \overline{f} \circ v )^{-1} ( V ) $)
est un ouvert de

( d'après la définition de la topologie quotient )

 = ( \overline{f} \circ v )^{-1} ( V ) $)
est un ouvert de



est continue.
Pouvez vous m'aider pour la question 2 ?
Merci infiniment. :happy3:
