Espace ordinaire

[legeniedesalpages]

Bonjour, j'ai du mal avec cet exo d'algèbre linéaire (j'ai oublié pas mal de notions d'algèbre, de géométrie planes et dans l'espace :briques: ) :

Dans l'espace ordinaire muni d'une origine , soient et une droite et un plan passant par .
1°) Trouver .
Soit la projection orthogonale de sur .
2°) Montrer que est un endomorphisme de ; trouver son noyau et son image.


Déjà, je ne me rappelle plus comment on définit une droite dans ce contexte, je n'arrive même pas à montrer que est un sous-espace de :

(ça c'est ok). Ensuite on prend deux points de la droite , et un scalaire .
Il faut que je montre que .

[kazeriahm]

je pense que ca dépend si tu définis une droite (ou un plan) plutot de manière algèbrique ou plutot de manière géomètrique

en algèbre, une droite c'et par définition un espace affine de dimension 1

un plan un espace affine de dimension 2

ici tes deux espaces contiennent l'origine donc ce sont des espaces vectoriels

[legeniedesalpages]

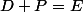
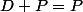
Avec ta définition c'est beaucoup plus simple, à ce moment-là ils sont évidemment des sous-espaces, et si , sinon.

Mais j'aurai voulu une définition plus "lycée" de la droite et du plan (je ne pe rappelle plus ce qu'on avait comme définition), en supposant les notions affines et la dimension encore inconnues.

En fait je voudrais savoir comment on peut se débrouiller à la main.

[kazeriahm]

bah sinon tu peux paramètrer ta droite comme on sait la faire au lycée, ce qui revient sans le dire à la considèrer comme un espace affine

il existe un vecteur directeur u de ta droite D

or elle passe par O l'origine

donc D={(x,y,z) dans R^3 / existe t réel, x=u_x*t, y=u_y*t et z=u_z*t}

donc D est un ev :)

pour le plan P tu peux considèrer une équation cartésienne de P

p:a*x+b*y+c*z=d

or (0,0,0) est dans P donc d=0 et tu as encore un ev puisque P={(x,y,z)/ a*x+b*y+c*z=0}

[legeniedesalpages]

ok, donc

si :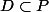

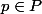
Soit . Il existe alors et tel que . Comme , .
Inversement, soit . On a .
Donc .

si n'est pas inclus dans :

Il est clair que . Par contre, je ne vois pas comment montrer que .

[kazeriahm]

bah tu peux raisonner sur la dimension (sans raisonner dessus explicitement)

si u est vecteur directeur de D, v et w base de P, alors il est clair que (u,v,w) est une base de E non ?

[legeniedesalpages]

oui, mais justement, je crois qu'en fait je dois montrer que trois vecteurs u,v,w engendrent E tout entier.

Il faudrait donc que je montre que E a besoin de seulement trois vecteurs (bien choisis) pour etre engendré; et que la famille (u,v,w) est libre, c'est ça?

[kazeriahm]

E est de dimension 3 par hypothese non ? qu'entends tu par espace ordinaire?

[legeniedesalpages]

Tu prends un vecteur x de l'espace, tu considères sa projection p(x) sur le plan parallèlement à la droite.

Salut Rain'.

Il me semble que pour que ta projection soit correctement définie, il faut avoir prouvé que D et P sont supplémentaires, non? :hein:

[legeniedesalpages]

Je ne sais pas justement ce que c'est exactement un espace ordinaire, c'est l'auteur qui utilise cette terminologie. Peut-être en référence à l'espace de la "géométrie dans l'espace" qu'on voit en terminale.

La seule chose que j'ai c'est ça:

L'ensemble des vecteurs libres de l'espace ordinaire est un espace vectoriel réel pour les opérations usuelles et . On peut identifier à l'espace ordinaire dans lequel on a choisi une origine , en faisant correspondre au point le vecteur .

[legeniedesalpages]

Merci Rain',

oui c'est exactement ce que je recherche.

Et en fait dès qu'on a choisi une origine , je pense que j'aurai du fixer une repère , comme ça on peut utiliser les coordonnées. :we:

[legeniedesalpages]

Soit la projection orthogonale de sur .
2°) Montrer que est un endomorphisme de ; trouver son noyau et son image.

Pour un point de , comment je peux exprimer ? :hein:

Je ne vois pas comment montrer que est un endomorphisme (il était temps que je me mette à l'algèbre :lol2: )

[legeniedesalpages]

ah mais en fait, je ne sais pas lire! haha

Dans l'énoncé D et P sont supposés perpendiculaires.

[legeniedesalpages]

Bon ben exercice résolu en fait :)