Espace metrisable

[barbu23]

Bonjour à tous,
Pourriez vous me rappeler de la definition d'un espace mertrisable avec quelque exemple possible ?
Merci d'avance; :happy3:

[arnaud32]

un espace metrisable est un espace topologique (E,T) ou la topologie peut etre decrite par une distance.

ex E non vide T=P(E) d(x,y) = 0 si x=y 1 sinon
les nombre reels et T= {]a,b[, a

[Ben314]

Salut,
Il me semble bien que la topologie associée à la distance discrète (d(x,y) = 0 si x=y 1 sinon), c'est la topologie discrète où T=P(X) (ensemble de toutes les parties de X) et pas la topologie grossière T={vide,X} qui n'est métrisable que lorsque X est un singleton.

Sinon, pour répondre à barbu23, "donner des exemples d'espaces métrisable", ben c'est trés con comme question : comme exemple, on va évidement te donner des espace métriques !!!
La question plus interessante est de donner des espaces non métrisables (et d'expliquer pourquoi ils ne le sont pas...)

[Nightmare]

On peut se rappeler pour exhiber un contre exemple que dans un espace métrique, on peut séparer les points.

[barbu23]

D'accord , alors un espace metrisable est tout simplement un espace metrique c'est à dire un espace topologique muni d'une metrique. c'est ça ? :doh:
Parceque un espace metrique est aussi un espace topologique dont les ouverts sont les parties telles que ? non ? :marteau:

[arnaud32]

un espace metrique est evidement metrisable.
un espace metrisable est en fait un espace homeomorphe a un espace metrique.

la question se pose plutot dans le sens suivant:
soit (E,T) un espace topologique, ou T est la famille des ouverts
peut on decrire T par une distance?

[Ben314]

Un exemple "un peu interessant" :

On considère l'ensemble constitué de toutes les parties de 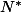ainsi que du complémentaire dans 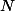de toutes les parties finies de .
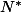1) Montrer que est l'ensemble des ouverts d'une certaine topologie sur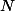
2) Montrer que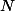 muni de cette topologie est métrisable.

[barbu23]

un espace metrique est evidement metrisable.
un espace metrisable est en fait un espace homeomorphe a un espace metrique.

la question se pose plutot dans le sens suivant:
soit (E,T) un espace topologique, ou T est la famille des ouverts
peut on decrire T par une distance?

D'accord !
D'où l'argument de Ben214 :
Existe -il des espaces non metrisables ?
Connaissez vous un exemple "simple" d'espace topologique qui ne peut pas être decrit par une metrique ?

MErci d'avance. :happy3:

[barbu23]

1) Montrer que est l'ensemble des ouverts d'une certaine topologie sur
.

ça veut dire qu'il faut trouver une topologie telle que , c'est ça ?
Si c'est comme ça, : topologie engendré par
:happy3:

[arnaud32]

comme te l'a indique nightmare, il suffit de trouver une topologie qui ne rend pas l'espace separe.
la topologie grossiere par ex.

[Ben314]

La question est :
"Montrer que est (le verbe être) l'ensemble des ouverts d'une certaine topologie sur "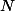
Cela signifie qu'il faut trouver une topologie telle que .

L'ambiguité vient du fait que j'aime pas bien dire qu'une topologie EST un ensemble d'ouverts car une topologie peut être définie de bien des façons diférentes et pas seulement par la donnée de l'ensemble de ces ouverts...

[barbu23]

La question est :
Cela signifie qu'il faut trouver une topologie telle que .

ça veut dire qu'il faut montrer simplement que est une topologie , non ??? :doh: :marteau:
Je ne sais pas la reponse pour cette question : :marteau: :we: