Espace des polynômes

par **marawita1** » 03 Oct 2015, 20:43

Pour

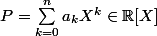
, on pose
N(P)=

1) vérifier que N est une norme sur R[X]
On pose

Vérifier que la suite P_n est de cauchy pour la norme N.
3) On suppose que la suite (P_n) converge et on note P sa limite.
Montrer qu'il existe un naturel d tel que

Pour 1) et 2) c'est bon, je suis bloqué au 3ème question.

Merci d'avance.

par **marawita1** » 04 Oct 2015, 16:47

S'il vous plait, qui a une réponse au 3eme question?
Merci.

par **zygomatique** » 04 Oct 2015, 17:04

salut

et si on posait d = deg(P) ....

REM : la définition de P_n est imprécise : on ne sait pas qui il est exactement car il manque un monome pour bien comprendre ....

par **marawita1** » 04 Oct 2015, 19:04

J'ai copié l'énoncé tel que l'est.
j'ai pas réussi à trouver l'inégalité demandé avec d= deg(P)

par **Doraki** » 04 Oct 2015, 19:44

Prend un polynôme P au hasard, par exemple P = 3 + 7X -5X² + 4X^3 ou alors P = X + X²/2 + X^3/3 + X^4/5,

et regarde les normes de (P-Pn) pour plusieurs n genre n=1,3,6,10,15,2000.

est-ce que tu remarques un truc.

par **marawita1** » 04 Oct 2015, 20:13

Franchement, j'ai pas remarqué un truc, mais bon j'ai essayé comme suit:

Soit n>d, on a
P_n - P=

deux cas possibles:
1) pour tout 1

et dans ce cas , on a || P_n - P||> 1/(d+1).

Donc dans tous les cas, on a pour tout n>d, || P_n - P||>= 1/(d+1).

C'est juste?

par **MMu** » 04 Oct 2015, 22:02

marawita1 a écrit:Franchement, j'ai pas remarqué un truc, mais bon j'ai essayé comme suit:

Soit n>d, on a
P_n - P=
deux cas possibles:
1) pour tout 1 et dans ce cas , on a || P_n - P||> 1/(d+1).

Donc dans tous les cas, on a pour tout n>d, || P_n - P||>= 1/(d+1).

C'est juste?

..
D'après la définition la norme d'un polynôme n'est jamais inférieure à ses coefficients , donc pour

on a

Je pense que le but de l'exercice est de montrer que l'espace

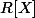
n'est pas complet . Vois tu pourquoi ?

par **marawita1** » 05 Oct 2015, 06:31

oui je vois.Merci bien.
Juste je veux savoir si l'explication que j'ai donnée est bonne ou non.

par **zygomatique** » 05 Oct 2015, 15:53

non elle ne vaut rien ...

sans utiliser l'argument de Mmu ::

soit il existe k = 1/(d + 1) alors par définition de ta norme c'est fini ...

soit il n'existe pas de tel k ... mezalor pour tout k > d + 1 :: 1/k < 1/(d + 1)et c'est à nouveau fini ...

par **Doraki** » 05 Oct 2015, 16:36

zygomatique a écrit:non elle ne vaut rien ...

sans utiliser l'argument de Mmu ::

soit il existe k = 1/(d + 1) alors par définition de ta norme c'est fini ...

soit il n'existe pas de tel k ... mezalor pour tout k > d + 1 :: 1/k < 1/(d + 1)et c'est à nouveau fini ...

sa preuve est correcte, même si elle est maladroite.

je comprends pas ta dernière ligne.

par **zygomatique** » 05 Oct 2015, 17:41

oui ... mais il manque tout de même l'argument de décroissance de la fonction inverse (dans son 1/) ce qui est ma dernière ligne ...

par **marawita1** » 05 Oct 2015, 18:59

Doraki a écrit:sa preuve est correcte, même si elle est maladroite.

je comprends pas ta dernière ligne.

J'ai pas compris pourquoi ma preuve est maladroite!!!!!!!!!!!!!!!!!!!!!!!!!

par **MMu** » 06 Oct 2015, 03:36

marawita1 a écrit:J'ai pas compris pourquoi ma preuve est maladroite!!!!!!!!!!!!!!!!!!!!!!!!!

Je dirais plutôt qu'elle est trop longue, mais elle marche .. :zen:

par **marawita1** » 06 Oct 2015, 08:37

MMu a écrit:Je dirais plutôt qu'elle est trop longue, mais elle marche .. :zen:

ok merci bien.

Espace des polynômes

Espace des polynômes

Qui est en ligne