Espace de Banach

[Archytas]

Salut,
Est ce que l'ensemble des endomorphismes continus inversibles d'inverse continu d'un Banach est ouvert pour la norme d'opérateur (la norme naturelle)? C'est assez facile en dimension finie avec la préimage du déterminant mais en dimension infinie ça semble moins évident.
Merci d'avance

[Ben314]

Salut,
La méthode classique consiste à montrer dans un premier temps que, si est linéaire continue et que alors la série est normalement convergente, donc convergente vu que l'ensemble des applications linéaires continues de E dans E est complet (où bien entendu, 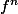désigne la composée de avec elle même fois).
Si on note sa somme, on vérifie aisément que est en fait l'inverse de ce qui montre que toute les applications linéaires continues qui sont dans la boule ouverte de centre et de rayon 1 sont inversible (et d'inverse continue).
On en déduit ensuite aisément que, si est linéaire continue inversible (d'inverse continue), il existe une boule ouverte centrée en ne contenant que des applications inversibles.
Je te laisse chercher quel est le rayon de cette boule (qui dépend évidement de ) pour que tout marche bien.

[Archytas]

Super j'ai saisi! En effet c'est moins simple qu'en dimension finie mais ça se saisi facilement!

Merci Ben!