[L1] Equivalents
34 messages
- Page 1 sur 2 - 1, 2
[L1] Equivalents
Salut a tous,
J ai quelques problemes avec des equivalents et je fais appel a vous :
1. On considere l equation e^x=nx avec n entier , cette equation possede 2 solution et on note y_n la plus grande j ai montrer que y_n est equivalent a ln(n) en l infini, òon probleme cest trouver un equivalent en l infini de y_n-ln(n) et j ai pas mieux que ln(y_n)
Comment peut on faire mieux ?
2. Soit l equation x^n=a(1-x) avec a reel et n entier
on note x_n la solution de cette equation pour tout n et v_n=1-x_n
a. Montrer que un equivalent de ln(v_n) en l infini est -n v_n
a. Montrer que un equivalent de ln(v_n) en l infini est -ln(n)
Je n y arrive pas , merci de votre aide ,
(Je suis a l etranger, penible le clavier :marteau: ... )
J ai quelques problemes avec des equivalents et je fais appel a vous :
1. On considere l equation e^x=nx avec n entier , cette equation possede 2 solution et on note y_n la plus grande j ai montrer que y_n est equivalent a ln(n) en l infini, òon probleme cest trouver un equivalent en l infini de y_n-ln(n) et j ai pas mieux que ln(y_n)
Comment peut on faire mieux ?
2. Soit l equation x^n=a(1-x) avec a reel et n entier
on note x_n la solution de cette equation pour tout n et v_n=1-x_n
a. Montrer que un equivalent de ln(v_n) en l infini est -n v_n
a. Montrer que un equivalent de ln(v_n) en l infini est -ln(n)
Je n y arrive pas , merci de votre aide ,
(Je suis a l etranger, penible le clavier :marteau: ... )
Salut !
C'est bon, c'est justifié,
Par contre pour la deuxième question je ne vois toujours pas ...
Je réécris par soucis de clarté avec des balises latex :
Soit n un entier naturel) une équation dont l'unique solution est notée
une équation dont l'unique solution est notée 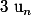 . On pose
. On pose 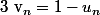 .
.
a. Montrer que \sim_{\infty} -nv_n)
b. Montrer que \sim_{\infty} -\ln(n))
c. En déduire un équivalent de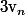 ( C'est fait. )
( C'est fait. )
Voilà, si quelqu'un peut m'aider pour la a et b, merci :we:
PS: Pour la a. tout est bon en fait, j'ai-ln(a)=ln(v_n)) mais bien sûr
mais bien sûr  \sim_{\infty} -nv_n) puis en divisant pas ln(v_n) on a notre équivalent facilement puisque ln(a)=o(ln(v_n))
puis en divisant pas ln(v_n) on a notre équivalent facilement puisque ln(a)=o(ln(v_n))
Si quelque sait pour le b ... merci :zen:
C'est bon, c'est justifié,
Par contre pour la deuxième question je ne vois toujours pas ...
Je réécris par soucis de clarté avec des balises latex :
Soit n un entier naturel
a. Montrer que
b. Montrer que
c. En déduire un équivalent de
Voilà, si quelqu'un peut m'aider pour la a et b, merci :we:
PS: Pour la a. tout est bon en fait, j'ai
Si quelque sait pour le b ... merci :zen:
benekire2 a écrit:Salut,
en 0 un équivalent de ln(1+x) est x or là v_n tend vers 0 d'où ln(1-v_n) équivalent à -v_n i.e nln(1-v_n) équivalent à -nv_n
Cela dit si tu me demande c'est qu'il y a une erreur, or je vois pas trop ... :doh:
Merci de ton aide nightmare :we:
Ce qui me gène, c'est que tu n'as prouvé nulle part que (vn) tendait vers 0 ! C'est quand même à écrire :lol3:
Bah en fait en regardant , on veut que cette limite vale 0:
}{ln(g)})
Et ça c'est du 0 X lim 1/ln(g) or si 1/ln(g) est bornée c'est gagné et si elle ne l'est pas alors on a une forme indéterminée et on est pas sûr que la limite fasse 0.
PS: Pour achever l'exercice, on montre que 1/ln(-ln(v_n)) --> 0 ce qui suffit pour dire que 1/ln(-ln(v_n)) est borné
Et ça c'est du 0 X lim 1/ln(g) or si 1/ln(g) est bornée c'est gagné et si elle ne l'est pas alors on a une forme indéterminée et on est pas sûr que la limite fasse 0.
PS: Pour achever l'exercice, on montre que 1/ln(-ln(v_n)) --> 0 ce qui suffit pour dire que 1/ln(-ln(v_n)) est borné
Salut,
Je reviens a la charge avec un nouvel équivalent a trouver, il s'agit de donner un équivalent en l'infini de :
)
Alors j'ai cherché et je vois pas du tout.
Par ailleurs j'avais vu un exercice ou on devait trouver un équivalent d'une somme et la correction utilisait des sommes de Riemann, j'espère que ici ce n'est pas le cas, parce que je ne connais pas les sommes de Riemann.
Si quelqu'un pouvait me donner des pistes,
Merci :happy3:
Je reviens a la charge avec un nouvel équivalent a trouver, il s'agit de donner un équivalent en l'infini de :
Alors j'ai cherché et je vois pas du tout.
Par ailleurs j'avais vu un exercice ou on devait trouver un équivalent d'une somme et la correction utilisait des sommes de Riemann, j'espère que ici ce n'est pas le cas, parce que je ne connais pas les sommes de Riemann.
Si quelqu'un pouvait me donner des pistes,
Merci :happy3:
re,
Une somme de Riemann de fonction positive est une somme d'aires de rectangles,
quasi aléatoire ou qu'on aimerait rendre aléatoire :we:
somme qui approxime l'aire située sous une courbe
Deux classes de fonctions réelles sont Riemann-intégrables: continues ou monotones
ici
La théorie a été rendue obsolète par:
1) Lebesgue
2) dernièrement par Kurzweil-Henstock
Une somme de Riemann de fonction positive est une somme d'aires de rectangles,
quasi aléatoire ou qu'on aimerait rendre aléatoire :we:
somme qui approxime l'aire située sous une courbe
Deux classes de fonctions réelles sont Riemann-intégrables: continues ou monotones
ici
La théorie a été rendue obsolète par:
1) Lebesgue
2) dernièrement par Kurzweil-Henstock
34 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 30 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
