Equivalents et calculs de limites..
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Benk
- Membre Relatif
- Messages: 128
- Enregistré le: 21 Sep 2006, 20:48
-
par Benk » 19 Nov 2009, 21:42
Bonjour,
voici deux équivalents à calculer..
Le premier est le suivant:
, équivalent à
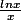
au voisinage de
, ce dont je suis plutôt sûr..
Je demande juste une petite vérification de votre part..
Par la suite, on me demande d'en déduire un équivalent toujours en
de:
J'ai un bout de l'historie je pense, en factorisant par x:
)
??
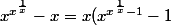Bonne soirée
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
par barbu23 » 19 Nov 2009, 21:46
Oui, exact ! :happy3:
-
Benk
- Membre Relatif
- Messages: 128
- Enregistré le: 21 Sep 2006, 20:48
-
par Benk » 19 Nov 2009, 21:56
barbu23 a écrit:Oui, exact ! :happy3:
mais comment continuer?
-
LoLLoLLoL
- Membre Naturel
- Messages: 40
- Enregistré le: 18 Nov 2009, 13:18
-
par LoLLoLLoL » 19 Nov 2009, 22:09
Equivalent ,equivalent , equivalent...
-
Benk
- Membre Relatif
- Messages: 128
- Enregistré le: 21 Sep 2006, 20:48
-
par Benk » 20 Nov 2009, 12:45
alavacommejetepousse a écrit:tu y es presque
recommence une fois tu trouves
)
Bonjour, je continue, et je trouve équivalent à x.. et non pas ln²(x) :mur:
est ce que ca vient de moi ou est-ce une erreur de ta part? (je pense plutot à la première option mais bon, sait-on jamais..
-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
par Ben314 » 20 Nov 2009, 14:56
Sans vouloir me meler de ce qui ne me regarde pas, je trouve aussi
\big)^2)
... (ca fait 2-1)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Benk
- Membre Relatif
- Messages: 128
- Enregistré le: 21 Sep 2006, 20:48
-
par Benk » 21 Nov 2009, 12:20
Oui c'est bon j'ai trouvé ln²(x)
Donc je récapitule
équivalent à
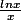
et
équivalent à
)^2)
au vois de + infini..
Mais maintenant, on me demande de déduire la limite
^{\frac{1}{x}}-x^{\frac{1}{x}}].(x.lnx)^2}{x^{x^{\frac{1}{x}}}-x })
Déja, on peut dire que cette expression est équivalente en
à
^{\frac{1}{x}}-x^{\frac{1}{x}}].x^2)
sacahnt les équivalents trouvés précédement..
Mais j'ai du mal à poursuivre, parce que l'expression est encore indéterminée, et je suis aussi bloqué au niveau de l'expression entre parenthèses.. des pistes?
-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
par Ben314 » 21 Nov 2009, 14:12
Une piste... met x^(1/x) en facteur dans la grande parenthèse....
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 31 invités
