Equivalent d'une suite bizarre
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 10 Oct 2009, 01:46
par Nightmare » 10 Oct 2009, 01:46
Salut à tous :happy3:
On considère la fonction
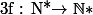
surjective, croissante et définie récursivement par
=card(f^{-1}(\{n\})))
.
Le but est de trouver un équivalent simple en +oo.
Je conjecture que c'est équivalent à
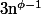
(nombre d'or) mais je ne trouve pas de preuve.
Avez-vous une idée?
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 10 Oct 2009, 06:22
par yos » 10 Oct 2009, 06:22
Salut.
Nightmare a écrit: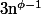
Au facteur
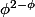
près... d'après Sloane.
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 10 Oct 2009, 06:54
par Doraki » 10 Oct 2009, 06:54
Si f est équivalente à quelquechose, on devrait avoir une équation du genre
f' ( F(x)) * f(x) = 1, où F est la primitive de f nulle en 0.
J'imagine que si on remplace f par un monôme, on obtient ce qu'on veut.
Mais c'est pas exactement une preuve.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 10 Oct 2009, 12:53
par Nightmare » 10 Oct 2009, 12:53
Salut à vous deux !
Doraki > Oui c'est comme ça que j'ai trouvé mon équivalent, en "affinant" le problème mais je ne trouve vraiment aucune preuve discrète ...
-
mathelot
 par mathelot » 10 Oct 2009, 14:37
par mathelot » 10 Oct 2009, 14:37
............................................
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 10 Oct 2009, 14:43
par Nightmare » 10 Oct 2009, 14:43
Salut !
Comme tu dis on sait que f(1)=1. La valeur 1 est prise f(1)=1 fois on en déduit que forcément f(2)=2. La valeur 2 est prise f(2) fois donc par croissance on a forcément f(3)=2.
La valeur 3 est donc prise f(3)=2 fois d'où f(4)=f(5)=3 etc..
-
mathelot
 par mathelot » 10 Oct 2009, 15:32
par mathelot » 10 Oct 2009, 15:32
oui, j'ai peiné !!!
dessinsoit le plan muni du repère orthonormal habituel
)
on marque les entiers de l'ensemble de départ
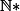
sur l'axe gradué
)
soit
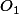
le point dde coordonnées (1,0).
on marque les images sur l'axe vertical
)
en empilant.
visuellement, ça donne une formule explicite de la suite
si
k}{2}+1 \leq n \leq \frac{k(k+1)}{2})
,alors
=k)
l'implication précedente est une équivalence.
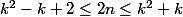
^2+\frac{7}{4} \leq 2n \leq (k+\frac{1}{2})^2-\frac{1}{4})
en remplaçant k par f(n):
 \leq \sqrt{2n -\frac{7}{4}}+\frac{1}{2})
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 10 Oct 2009, 15:45
par Nightmare » 10 Oct 2009, 15:45
Soit j'ai mal fait mon dessin , soit je ne vois vraiment pas comment tu obtiens ton encadrement à partir de celui-ci !
Toujours étant, tu trouves donc f équivalente à sqrt(2n), bizarre !
-
mathelot
 par mathelot » 10 Oct 2009, 19:27
par mathelot » 10 Oct 2009, 19:27
re,
1 (image) a exactement 1 antécédent {1}
2 (image) a exactement 2 antécédents {2;3}
3 (image) a exactement 3 antécédents {4;5;6}
4 (image) a exactement 4 antécédents {7;8;9;10}
il y a donc
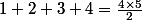
éléments dans
)
on voit qu'il y a une formule avec le 1er polynôme de Bernoulli
pour caractériser les antécédents appartenant à
)
i
-
wserdx
- Membre Rationnel
- Messages: 654
- Enregistré le: 03 Oct 2009, 13:44
-
 par wserdx » 10 Oct 2009, 21:14
par wserdx » 10 Oct 2009, 21:14
Non, pas d'accord,
\\<br />1 \to 1\\<br />2 \to 2\\<br />3 \to 2\\<br />4 \to 3\\<br />5 \to 3\\<br />6 \to 4\\<br />7 \to 4\\<br />8 \to 4\\<br />9 \to 5\\<br />10 \to 5\\<br />11 \to 5\\<br />12 \to 6\\<br />13 \to 6\\<br />14 \to 6\\<br />15 \to 6\\<br />16 \to 7\\<br />17 \to 7\\<br />18 \to 7\\<br />\ldots)
J'en ai déduit la formule suivante
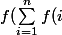}) = n)
Suit une démonstration "à la hache" :
Si on suppose qu'il existe

et

tels que
 \sim \alpha n^\beta)
alors
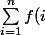} \sim \alpha n^{\beta+1}/(\beta + 1))
Donc on doit avoir
)^\beta \sim n)
soit
\beta = 1)
soit
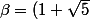/2)
-
mathelot
 par mathelot » 10 Oct 2009, 22:16
par mathelot » 10 Oct 2009, 22:16
bonsoir,
j'étais parti sur
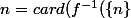))
autant pour moi. :hum: je me suis trompé.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 73 invités