Equivalent
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
guillaume100
- Membre Naturel
- Messages: 97
- Enregistré le: 29 Déc 2018, 14:49
-
 par guillaume100 » 28 Mai 2019, 13:31
par guillaume100 » 28 Mai 2019, 13:31
Bonjour à tous,
Comment trouver un developement asymptotique à 2 termes de la suite verifiant :
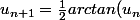)
NB: je trouve u(n) equivaut à alpha/2^n mais j'arrive pas à trouver le alpha
-
pascal16
- Membre Légendaire
- Messages: 6663
- Enregistré le: 01 Mar 2017, 12:58
- Localisation: Angoulème : Ville de la BD et du FFA. gare TGV
-
 par pascal16 » 29 Mai 2019, 17:58
par pascal16 » 29 Mai 2019, 17:58
1/ tu as sans doute démontré que la limite était 0.
le DL en 0 de arctang peut sans doute te donner une piste
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 29 Mai 2019, 19:03
par GaBuZoMeu » 29 Mai 2019, 19:03
Quel sens cela pourrait-il avoir de "trouver le

" ?
Si

a pour limite

, alors la suite décalée
)
définie par
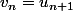
vérifie la même relation de récurrence, et elle vérifie
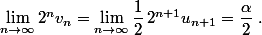
-
Tuvasbien
- Membre Relatif
- Messages: 440
- Enregistré le: 28 Fév 2019, 00:59
-
 par Tuvasbien » 29 Mai 2019, 19:28
par Tuvasbien » 29 Mai 2019, 19:28
Je pense que ton raisonnement est le suivant : Si
_{n\in\mathbb{N}})
converge, alors elle converge vers le seul point fixe de arctan à savoir 0. Il s'ensuit que
\sim u_n)
d'où

puis finalement

avec
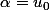
. Là où ça bloque c'est sur le "finalement", par exemple,

et pourtant
^n)
tend vers

alors que
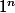
tend vers 1. Les relations de récurrence sur les équivalents ça marche pas forcément très bien à cause de la forme indéterminée
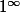
.
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 29 Mai 2019, 19:58
par Skullkid » 29 Mai 2019, 19:58
Bonsoir,
Par rapport à la question sur le deuxième terme du développement, tu peux te servir des théorèmes de sommation des relations de comparaison (en exploitant le lien entre une suite et la série de ses différences).
-
guillaume100
- Membre Naturel
- Messages: 97
- Enregistré le: 29 Déc 2018, 14:49
-
 par guillaume100 » 30 Mai 2019, 05:08
par guillaume100 » 30 Mai 2019, 05:08
Merci pour vos reponses !
En considérant

et en effectuant un developpement limité (asymptotique) à l'ordre 3 et en sommant sur le reste des sommes partielles on obtient le deuxiele terme du DL
-
LB2
- Habitué(e)
- Messages: 1504
- Enregistré le: 05 Nov 2017, 16:32
-
 par LB2 » 30 Mai 2019, 21:03
par LB2 » 30 Mai 2019, 21:03
Bonjour,
il y a souvent un argument "Cesaro like" dans ce genre d'exercices : si la suite

tend vers

, alors par Cesaro

tend aussi vers

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 23 invités