Équivalent à ln(2x³-3x²+1) en +oo
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Hick_Jeck
- Membre Relatif
- Messages: 111
- Enregistré le: 11 Mar 2008, 21:17
-
 par Hick_Jeck » 13 Déc 2010, 20:23
par Hick_Jeck » 13 Déc 2010, 20:23
Bonjour,
Je dois trouve un équivalent à ln(2x³-3x²+1) en +infini. Je devais trouver d'abord en 0 (ce que j'ai fait grâce à un développement limité et j'ai trouvé -3x² à l'ordre minimum (2)). En + infini, c'est une autre paire de manche... J'ai essayé un changement de variable qui n'aboutit pas à cause du +1 forcément.
Si vous avez une idée, n'hésitez pas,
Hick_Jeck
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 13 Déc 2010, 20:46
par Arnaud-29-31 » 13 Déc 2010, 20:46
Salut,
Il faut factoriser :
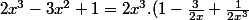)
-
Hick_Jeck
- Membre Relatif
- Messages: 111
- Enregistré le: 11 Mar 2008, 21:17
-
 par Hick_Jeck » 13 Déc 2010, 21:34
par Hick_Jeck » 13 Déc 2010, 21:34
Effectivement, merci :) .
-
bentaarito
- Membre Rationnel
- Messages: 603
- Enregistré le: 30 Oct 2009, 01:58
-
 par bentaarito » 13 Déc 2010, 23:30
par bentaarito » 13 Déc 2010, 23:30
et tu trouves quoi finalement??
-
bentaarito
- Membre Rationnel
- Messages: 603
- Enregistré le: 30 Oct 2009, 01:58
-
 par bentaarito » 14 Déc 2010, 00:04
par bentaarito » 14 Déc 2010, 00:04
quelqu'un peut me répondre pare que je vois pas comment on peut faire ici!! :hum:
-
Euler07
- Membre Irrationnel
- Messages: 1157
- Enregistré le: 25 Avr 2009, 11:00
-
 par Euler07 » 14 Déc 2010, 00:09
par Euler07 » 14 Déc 2010, 00:09
ln(1-x) tend vers x au voisinage de 0
-
bentaarito
- Membre Rationnel
- Messages: 603
- Enregistré le: 30 Oct 2009, 01:58
-
 par bentaarito » 14 Déc 2010, 00:12
par bentaarito » 14 Déc 2010, 00:12
je parle d'un ~ en

&
alors pas de réponse???
-
bentaarito
- Membre Rationnel
- Messages: 603
- Enregistré le: 30 Oct 2009, 01:58
-
 par bentaarito » 14 Déc 2010, 00:27
par bentaarito » 14 Déc 2010, 00:27
alors!!!! :happy2:
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 14 Déc 2010, 08:36
par Arnaud-29-31 » 14 Déc 2010, 08:36
Bein on factorise,
 = ln \left( 2x^3.(1 - \frac{3}{2x} + \frac{1}{2x^3}) \right) = ln(2x^3) + ln \left( 1 - \frac{3}{2x} + \frac{1}{2x^3} \right))
-
bentaarito
- Membre Rationnel
- Messages: 603
- Enregistré le: 30 Oct 2009, 01:58
-
 par bentaarito » 14 Déc 2010, 15:12
par bentaarito » 14 Déc 2010, 15:12
oui exactement, mais je vois pas comment on fait pour
)
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 14 Déc 2010, 15:20
par Sylviel » 14 Déc 2010, 15:20
et les propriétés basiques du logarithme sont déjà oubliées :lol3: ?
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
bentaarito
- Membre Rationnel
- Messages: 603
- Enregistré le: 30 Oct 2009, 01:58
-
 par bentaarito » 14 Déc 2010, 15:31
par bentaarito » 14 Déc 2010, 15:31
je connais bien les propriétés du log. nep. mais le DL en

, ça m'échappe !!!!!
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 14 Déc 2010, 15:34
par Arnaud-29-31 » 14 Déc 2010, 15:34
Comment ca comment on fait pour
)
? Bein on le laisse tranquille ... et le deuxième terme en du style ln(1+u) avec u qui tend vers zéro en l'infini donc on peut faire un développement ...
Ceci te permet de proposer un développement limité, maintenant si tu veux juste un équivalent, c'est immédiat :

et
 \underset{\infty}{\sim} ln(2x^3))
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 14 Déc 2010, 15:34
par ffpower » 14 Déc 2010, 15:34
Si tu connais bien; alors applique les ici et vois ce que ca donne..
-
bentaarito
- Membre Rationnel
- Messages: 603
- Enregistré le: 30 Oct 2009, 01:58
-
 par bentaarito » 14 Déc 2010, 15:37
par bentaarito » 14 Déc 2010, 15:37
Arnaud-29-31 a écrit:Comment ca comment on fait pour
)
? Bein on le laisse tranquille ... et le deuxième terme en du style ln(1+u) avec u qui tend vers zéro en l'infini donc on peut faire un développement ...
Ceci te permet de proposer un développement limité, maintenant si tu veux juste un équivalent, c'est immédiat :

et
 \underset{\infty}{\sim} ln(2x^3))
oui ça je le sais
mais y a pas un ~ de

en

??????
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 14 Déc 2010, 15:59
par Arnaud-29-31 » 14 Déc 2010, 15:59
Tu voudrais écrire ln(x) comme une somme de puissances de x + un petit o ?
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 14 Déc 2010, 16:04
par Sylviel » 14 Déc 2010, 16:04
ln(x^3)=3ln(x) et tu ne feras pas mieux.
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 14 Déc 2010, 16:09
par Arnaud-29-31 » 14 Déc 2010, 16:09
}{x^n} = 0)
pour tout n ... autrement dit, la fonction logarithme devient ridicule devant n'importe quelle puissance de x.
On aura donc du mal à écrire quelque chose du type
 = a.x^{n_1} + b.x^{n_2} + o(x^{n_2}))
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 14 Déc 2010, 16:12
par Sylviel » 14 Déc 2010, 16:12
si on peut toujours écrire ln(x)=o(x) :ptdr:
Mais ça te donneras pas d'équivalent ça.
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
bentaarito
- Membre Rationnel
- Messages: 603
- Enregistré le: 30 Oct 2009, 01:58
-
 par bentaarito » 14 Déc 2010, 16:22
par bentaarito » 14 Déc 2010, 16:22
oui c'est clair, c'est ce que je me disais aussi :lol3:
mais la question tel qu'il l'a posée ,Hick_Jeck, m'a parue un peu perturbante
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 56 invités
? Bein on le laisse tranquille ... et le deuxième terme en du style ln(1+u) avec u qui tend vers zéro en l'infini donc on peut faire un développement ...
et
