Équivalent suite d'intégrales
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
roket
- Messages: 5
- Enregistré le: 04 Jan 2015, 13:35
-
 par roket » 06 Avr 2015, 12:24
par roket » 06 Avr 2015, 12:24
Bonjour, je pêche sur une étape dans l'exercice suivant :
Donner la limite et un équivalent de :
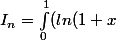)^ndx)
La suite est décroissante, minorée elle converge.
J'ai trouvé la relation de récurrence :
I_{n} = 2ln(2)^{n+1})
La suite tend vers 0 car sinon (n+1)In --> +inf alors que ce qui reste dans l'égalité est un O(1).
On obtient aussi :
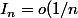)
Cependant, je n'arrive pas à justifier

Pour dire :
^n}{n})
Pouvez vous m'aider

)
Merci!

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 06 Avr 2015, 13:34
par Ben314 » 06 Avr 2015, 13:34
Salut,
Je sais pas comment faire uniquement en partant de la formule de récurrence

,
MAIS,
En posant
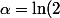)
et
}{\alpha}\)
il vient


çe qui montre déjà que
)
.
De même, le fait que
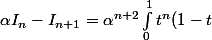e^{\alpha t}dt)
montre que
(n+2)}\leq \alpha I_n-I_{n+1}\leq\frac{2\alpha^{n+2}}{(n+1)(n+2))
ce qui, grâce à (1), prouve que
}\leq\alpha I_n-I_{n+1}\leq\frac{2\alpha I_n}{n+2})
c'est à dire que
)
donc en particulier que

.
Si tu injecte ça dans ta formule de récurrence, ça te permet effectivement de conclure.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
roket
- Messages: 5
- Enregistré le: 04 Jan 2015, 13:35
-
 par roket » 06 Avr 2015, 14:45
par roket » 06 Avr 2015, 14:45
Merci pour la méthode, je n'avais pas vu déjà que In était équivalent à alpha In....

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 06 Avr 2015, 15:25
par Ben314 » 06 Avr 2015, 15:25
roket a écrit:...
Pour dire :
^n}{n})
Pourtant, le fait que

implique que

Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 06 Avr 2015, 15:38
par Ben314 » 06 Avr 2015, 15:38
Et en réfléchissant un peu plus, en fait tu n'as même pas besoin de cet équivalent.
La décroissance ce la suite
_{n\geq0})
suffit pour conclure :
Ta formule
I_{n} = 2\alpha^{n+1}\)
dit que

Or

donc

Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
roket
- Messages: 5
- Enregistré le: 04 Jan 2015, 13:35
-
 par roket » 06 Avr 2015, 15:59
par roket » 06 Avr 2015, 15:59
Ben314 a écrit:Et en réfléchissant un peu plus, en fait tu n'as même pas besoin de cet équivalent.
La décroissance ce la suite
_{n\geq0})
suffit pour conclure :
Ta formule
I_{n} = 2\alpha^{n+1}\)
dit que

Or

donc

Merci beaucoup !! J'avais pas réussi à exploiter la décroissance qui me semble être le truc pratique dans tous les exos de ce type. Merci pour ton temps et tes explications limpides

)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 38 invités
