Bonjour nuage et bonjour tize,
Merci pour le lien fourni,
J'ai pu enfin trouver une correction détaillée pour la série de terme général:

Ma première intuition était la bonne:on pouvait en effet appliquer le critère de d'Alembert,mais je n'avais pas poursuivi le calcul assez loin pour pouvoir conclure:
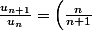^n)

quand
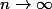
Donc la série converge bien car 1/e=0,3678<1
Une autre série me pose problème c'est celle de terme général:
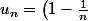^n)
Pour cette derniére,le critère de Cauchy est pris en défaut:

quand
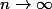
Je ne vois donc pas non plus quel critère ou équivalent utiliser....
En fait cette série diverge grossièrement,mais comment le prouver?
