Comment trouve t-on un équivalent de
équivalent intégrale
7 messages
- Page 1 sur 1
équivalent intégrale
par lisonn » 19 Oct 2011, 08:43
Bonjour,
Comment trouve t-on un équivalent de
quand u tend vers l'infini ?
Comment trouve t-on un équivalent de
par busard_des_roseaux » 19 Oct 2011, 22:38
Bonsoir,
je suis intéréssé par la réponse , je ne sais plus faire .il me semble que Dieudonné , in "Calcul infinitésimal, Chap 3 développement asymptotiques", indique comment primitiver les équivalents.
je suis intéréssé par la réponse , je ne sais plus faire .il me semble que Dieudonné , in "Calcul infinitésimal, Chap 3 développement asymptotiques", indique comment primitiver les équivalents.
par Skullkid » 20 Oct 2011, 00:14
Bonsoir, il y a en effet des théorèmes d'intégration des relations de comparaison, et l'un d'entre eux dit que si f et g sont deux fonctions continues par morceaux définies sur I = [a,+l'infini[ telles que g est positive sur I, intégrable sur I, et équivalente à f en l'infini, alors f est intégrable sur I et 
.
Le souci c'est qu'on a pas d'équivalent simple de
autre que lui-même, donc le théorème n'avance à rien. "Sortir" le 1/x et le remplacer par un 1/u comme tu l'as fait ne se justifie pas. Cependant cette démarche heuristique n'est pas inutile car elle permet de trouver le bon équivalent, qui est en effet 
.
Un moyen possible pour trouver des équivalents d'intégrales est l'intégration par parties. Elle permet parfois d'écrire une intégrale comme somme d'un terme dominant et d'une autre intégrale qui sera négligeable (typiquement, en l'infini, une intégration par parties peut faire chuter les exposants dans l'intégrande). La forme telle quelle de l'intégrale n'est pas très adaptée à une intégration par parties, donc on va d'abord faire un changement de variable, pour u assez grand (et t strictement positif, cela va de soi) :
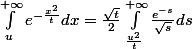
Et là on est content parce que dans l'intégrale on a une exponentielle fois une puissance qu'on va pouvoir faire chuter en intégrant par parties.
Le souci c'est qu'on a pas d'équivalent simple de
Un moyen possible pour trouver des équivalents d'intégrales est l'intégration par parties. Elle permet parfois d'écrire une intégrale comme somme d'un terme dominant et d'une autre intégrale qui sera négligeable (typiquement, en l'infini, une intégration par parties peut faire chuter les exposants dans l'intégrande). La forme telle quelle de l'intégrale n'est pas très adaptée à une intégration par parties, donc on va d'abord faire un changement de variable, pour u assez grand (et t strictement positif, cela va de soi) :
Et là on est content parce que dans l'intégrale on a une exponentielle fois une puissance qu'on va pouvoir faire chuter en intégrant par parties.
par busard_des_roseaux » 20 Oct 2011, 07:56
ok, merci. Est-ce que l'on peut utiliser également le 2ème théorème de la moyenne ?
par Skullkid » 20 Oct 2011, 13:19
Si mes souvenirs sont bons, ce théorème n'est valable que sur un segment. On pourrait s'en servir pour écrire 
avec u²/t < c < A, mais on ne sait pas ce qui arrive à c quand A tend vers l'infini.
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 36 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :