Equivalence au voisinage de a

par **tony800** » 30 Nov 2007, 13:00

Bonjour,

Je bloque sur une petite question.
La voici : Montrer que cet fonction est équivalente au voisinage de a :

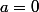
J'obtiens une forme indéterminé quand je calcul :

.

Mais je ne vois pas comment levé l'indétermination.
Est-ce que quelqu'un peut m'aider?
Merci d'avance.
Au revoir.

par **SimonB** » 30 Nov 2007, 13:09

Connais-tu les développements limités ?

par **tony800** » 30 Nov 2007, 13:14

Je ne crois pas ou alors sous un autre nom (mais cela m'étonnerait).
Vous pouvez toujours me dire en quoi cela consiste, peut être que je comprendrai.

par **tize** » 30 Nov 2007, 13:15

Bonjour,

la limite en zéro est donc la somme des dérivées de deux fonctions en zéro...

par **tony800** » 30 Nov 2007, 13:19

Je viens de regarder dans mon cours et on s'est arrêté au théorèmes des accroissements finis.

par **tony800** » 30 Nov 2007, 13:27

Je suis d'accord avec cela mais comment montrer que :

EDIT : je crois que j'ai compris merci de la rapidité de vos réponses ainsi que pour l'aide que vous m'avez apporté.

par **BertrandR** » 30 Nov 2007, 18:07

Je ne suis pas sur des condition de son application, mais si tu ne connais pas encore les developpements limité, tu peux utiliser la règle de lhopitale (je connais pas l'orthographe dsl) qui consiste pour trouver cette limite en 0 à chercher la limite des sa dérivée. A priori ca devrai marcher. Mais de toute facon tu feras bientot les developpement limité et tu n'en aura plus besoin ^^

par **The Void** » 30 Nov 2007, 21:47

tony800 a écrit:Je suis d'accord avec cela mais comment montrer que :

EDIT : je crois que j'ai compris merci de la rapidité de vos réponses ainsi que pour l'aide que vous m'avez apporté.

Salut,
Si tu préfères,

et sin(X)/X -> 1 en 0.

Equivalence au voisinage de a

Equivalence au voisinage de a

Qui est en ligne