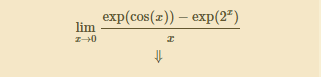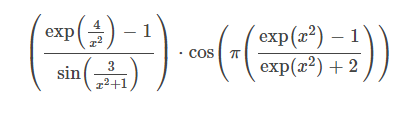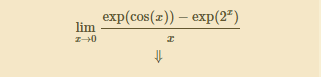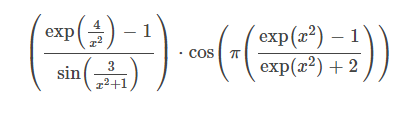Equivalence d'une fonction
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Youssri
- Membre Naturel
- Messages: 46
- Enregistré le: 08 Aoû 2018, 09:29
-
 par Youssri » 30 Oct 2018, 08:49
par Youssri » 30 Oct 2018, 08:49
Bonjour,
quelle astuce pour determiner ces equivalences?:
1/ en 0 de:
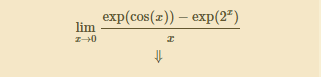
RP : je coince a ce niveau la f()~(cos(x) - 2^x)/x
1/ en l'infi de:
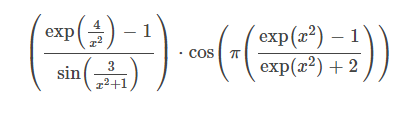
RP : le premier () est facile, le cos() est plus compliquer
-
hdci
- Membre Irrationnel
- Messages: 1962
- Enregistré le: 23 Juin 2018, 16:13
-
 par hdci » 30 Oct 2018, 09:33
par hdci » 30 Oct 2018, 09:33
Bonjour,
Pour la première équivalence, passer par les développements limités ?
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
-
Youssri
- Membre Naturel
- Messages: 46
- Enregistré le: 08 Aoû 2018, 09:29
-
 par Youssri » 30 Oct 2018, 09:44
par Youssri » 30 Oct 2018, 09:44
c'est quoi de DL? lol haha.
-
hdci
- Membre Irrationnel
- Messages: 1962
- Enregistré le: 23 Juin 2018, 16:13
-
 par hdci » 30 Oct 2018, 09:49
par hdci » 30 Oct 2018, 09:49
"Développement limité".
Par exemple,
=1-\dfrac{x^2}{2}+o(x^2))
Mais si vous n'avez pas vu cela, il faut trouver une autre solution (dommage, par les DL la première s'obtient facilement)
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
-
aviateur
 par aviateur » 30 Oct 2018, 11:28
par aviateur » 30 Oct 2018, 11:28
Bonjour
Pour le 1) il faut poser f(x) le numérateur et comme f(0)=0, la limite c'est f'(0) qu'il faut calculer.
Pour le deuxième c'est pareil. L'équivalent c'est la limite, le cos tend évidemment par -1 et le facteur devant vers 4/3 (limite obtenue grâce a des équivalent simples provenant de la dérivabilité des fcts exp et sin)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 39 invités