Equivalence de normes sur les polynômes

[zwijndrecht]

Bonsoir,

Pour un polynôme , on définit et .

On montre assez facilement (inégalité triangulaire) que , mais a-t-on , pour un certain ne dépendant pas du degré de ?

Je sais que les espaces de polynômes sont souvent de bons candidats pour montrer qu'en dimension infinie, toutes les normes ne sont pas équivalentes, et qu'on procède souvent en construisant une suite qui fait "exploser" l'une des deux normes (typiquement, , qui vérifie ). Mais là, je ne vois pas ce qui empêcherait "d'exploser" elle aussi en même temps que ...

Auriez-vous une piste à me donner ?

Merci d'avance.

[Ben314]

Salut,
Je sais pas si ça marcherais pas avec ça : (avec ) :
lorsque .
Si
et je me demande si ça reste pas borné du fait que .
Mais c'est à vérifier proprement (et il y a peut-être plus simple . . .)

[zwijndrecht]

Merci pour ta réponse.

Le problème, c'est que la série ne converge a priori pas uniformément en sur l'intervalle ...

Pour calculer la somme de série, j'utilise la série de Fourier de la fonction impaire et périodique définie par sur (continue en , mais discontinue en ...).

Les coefficients de Fourrier "réels" en cosinus sont nuls (par imparité de ), ceux en sinus valent , et comme est périodqie et par morceaux, le théorème de Dirichlet donne la convergence simple de vers pour , et vers sinon.

Mais le point de discontinuité en empêche d'appliquer le critère qui donne la convergence normale (et donc uniforme) sur (on l'a juste sur tout intervalle de la forme , où .

Du coup, j'ai essayé avec le critère d'Abel uniforme :
- converge (uniformément) vers en décroissant ;
- Par contre, pour montrer que l'on peut borner la suite des sommes partielles par une borne indépendante de , là encore, on a besoin de se placer un intervalle de la forme (le problème subsiste en 0).

[Ben314]

Concernant la majoration, j'ai aussi tenté plusieurs approches (en particulier... les mêmes que toi) sans pouvoir aboutir alors que si tu trace les fonctions pour un certain nombre de valeurs de , ça semble on ne peut plus borné : il y a juste le "phénomène de Gibbs" qui fait que ça "déborde" de la fonction limite , mais comme toujours, le "débordement" ne s'amplifie pas du tout lorsque augmente.

J'ai vaguement regardé aussi qu'on trouve facilement les zéros de la dérivée de , mais je suis pas allé plus loin en cherchant à les réinjecter dans (c'est à peine bourrin comme calculs . . .)
J'ai aussi vaguement cherché sur le net avec des truc style "majoration des restes dans une série de Fourrier" sans rien trouver de pertinent alors que la question semble somme toute "assez naturelle". Mais bon, j'ai peut-être pas cherché aux bons endroits . . .

J'ai aussi cherché d'autres exemples susceptibles de prouver que les normes ne sont pas équivalentes en espérant en trouver avec des calculs moins délicats, mais jusque là, c'est chou blanc . . .

EDIT : Peut-être en cherchant "phénomène de Gibbs" sur le Net : si on trouve autres chose que de simples dessins il y aurait sans doute des idées à piocher pour voir comment majorer . . .

[Ben314]

En fait, ça à l'air de se faire avec les dérivées :
Sur les max. locaux de sont aux points avec .
Pour , en écrivant que on arrive à montrer que ce qui prouve que le max. de sur est en .
Sauf que la majoration montre que

[zwijndrecht]

Comment trouves-tu que les maxima locaux de sont ces points ?
Pour la dérivée, je trouve , avec pour points d'annulation sur les points , mais aussi les points .

Pour montrer que les sont des maxima locaux, j'imagine qu'il faut passer par la dérivée seconde (en montrant qu'elle est négative en ces points), mais pour montrer que les n'en sont pas ?
D'ailleurs, en parlant de la dérivée seconde, je galère un peu à trouver une expression simple à manier... Pour , je trouve , mais ce n'est pas très facile d'étudier le signe de cette expression (et je ne vois pas trop comment je pourrais factoriser tout ça...).

Sinon, pour revenir sur le phénomène de Gibbs, il semblerait que l'oscillation autour du point de discontinuité soit bornée par 0.09*amplitude de la discontinuité ( https://en.wikipedia.org/wiki/Gibbs_phenomenon). En particulier, ici, l'oscillation varierait dans l'intervalle . Par contre, je n'ai pas trouvé de preuve complète de ce résultat. J'étais donc en train de reprendre la preuve proposée (sur un cas particulier assez proche du nôtre !) dans la section "Square wave analysis" en essayant de l'adapter à notre cas. Dans ce cas, seul le premier extremum local nous intéresse (car ensuite, on utilise la convergence uniforme sur ), mais je bloque sur la dérivée seconde...

[Ben314]

Comment trouves-tu que les maxima locaux de sont ces points ?
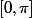
. . . avec pour points d'annulation sur les points , mais aussi les points .

Ca marche peut-être avec la dérivée seconde, mais on peut le faire aussi "à la rustique" vu que,
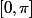
sur l'intervalle (pas plus), les zéro de la dérivée sont dans cet ordre là :

(l'inégalité bleue est triviale et la rouge équivaut à donc à )
Et comme la dérivée change de signe à chaque fois qu'elle s'annule, et qu'elle est positive en 0 les max. locaux, c'est bien les et les sont des min. locaux. (par contre ça s'inverse une fois passé mais ça c'était évident dés le départ par symétrie)

Dans ce cas, seul le premier extremum local nous intéresse (car ensuite, on utilise la convergence uniforme sur )

Attention, ça marche pas ça vu que tend vers 0.

Sinon, un autre point un peu chiant, c'est de montrer que, pour on a :



par décroissance de la fonction sur .
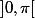
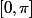
Donc le max. absolu de sur c'est .
Et, par symétrie, le min. absolu de sur , c'est mais par contre, je ne sais pas si on peut se passer d'une étude similaire pour les autres zéros de la dérivée (ceux de la forme ) pour en conclure que ces deux valeurs sont bien le max. et la min. de sur . . .

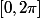
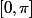
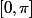
EDIT : je viens de regarder que les calculs pour les sont quasi les mêmes avec de nouveau donc, si est pair, le min. absolu de sur est et, pour impair, le min. absolu sur est soit , soit et on peut montrer que (ou utiliser le fait qu'on est dans une zone de convergence normale de la fonction).

Le bilan, c'est que ça marche, mais c'est tout de même passablement fastidieux et j'aimerais bien savoir s'il n'y a pas un exemple plus "élémentaire" . . .

[Ben314]

Sinon, concernant le phénomène de Gibbs, là on a tout ce qu'il faut pour faire la preuve générale :
Pour fixé lorsque (somme de Riemann)
et et on vérifie facilement que :

Ce qui signifie bien que la fonction fait des oscillations autour de la valeur et que la valeur de ces oscillations (en plus ou en moins) tend vers des constantes.
Par exemple la première oscillation dépasse de soit une augmentation relative par rapport à la hauteur de la discontinuité de et on peut évaluer de même ; ; . . .

Et si on part d'une fonction -périodique, par morceaux et ayant une discontinuité en alors on peut :
- Ramener la discontinuité en 0 par translation sur l'axe des x (ce qui ne fait que translater les sommes de Fourier)
- Se débrouiller pour avoir par translation sur l'axe des y (ce qui ne fait que translater les sommes de Fourier)
- Gommer le discontinuité en retranchant où est la "hauteur" de la discontinuité.
La nouvelle fonction obtenue est continue en 0 donc ces sommes de Fourier convergent uniformément vers la fonction au voisinage de 0 et ça montre que le "défaut de convergence uniforme" de la série de Fourier de au voisinage de est le même que celui de au voisinage de 0 avec en particulier les même "débordement" de +8,95% puis -4,86% puis +3,3% etc . . .

[zwijndrecht]

Ok, merci beaucoup ! Effectivement, ça fait pas mal de calculs assez long à écrire si l'on veut tout écrire proprement, mais on y arrive...

on vérifie facilement que :

Juste pour être sûr, ici, tu utilises le théorème des suites adjacentes, ou il y a un truc plus flagrant ? (j'ai pas mal galéré à justifier ce passage, et je ne vois finalement que ça comme justification...) :

Et si on part d'une fonction -périodique, par morceaux et ayant une discontinuité en alors on peut :
- Ramener la discontinuité en 0 par translation sur l'axe des x (ce qui ne fait que translater les sommes de Fourier)
- Se débrouiller pour avoir par translation sur l'axe des y (ce qui ne fait que translater les sommes de Fourier)
- Gommer le discontinuité en retranchant où est la "hauteur" de la discontinuité.
La nouvelle fonction obtenue est continue en 0 donc ces sommes de Fourier convergent uniformément vers la fonction au voisinage de 0 et ça montre que le "défaut de convergence uniforme" de la série de Fourier de au voisinage de est le même que celui de au voisinage de 0 avec en particulier les même "débordement" de +8,95% puis -4,86% puis +3,3% etc . . .

Maintenant, je comprends mieux pourquoi sur Wikipédia, ils se contentent de traiter le cas du signal "carré" (qui semble un peu plus simple à manier)... Ils manque juste ces quelques lignes à la fin pour prouver le théorème général !

Du coup, modulo la connaissance de ce résultat "général" (mais qui ne figure pas dans la plupart des cours sur les séries de Fourier), l'exemple n'est pas si fastidieux à traiter
En tout cas, merci encore. En plus d'avoir la réponse à ma question, j'ai appris un truc (assez sympa) sur les séries de Fourrier

[Ben314]

Juste pour être sûr, ici, tu utilises le théorème des suites adjacentes, ou il y a un truc plus flagrant ? (j'ai pas mal galéré à justifier ce passage, et je ne vois finalement que ça comme justification...) :

A la main, c'est pas difficile non plus vu que et sont de la forme

où le premier terme du produit reste de signe constant (dépendant de la parité de ) et le second est .

Du coup, modulo la connaissance de ce résultat "général" (mais qui ne figure pas dans la plupart des cours sur les séries de Fourier), l'exemple n'est pas si fastidieux à traiter

C'est pas faux : si on connait le résultat de Gibbs, la premier message (de 5 lignes) suffit.
Et sinon, perso., c'est pareil : lorsque j'était étudiant (il y a fort longtemps...) il ne me semble pas avoir entendu parler du phénomène de Gibbs. Mais je pense que c'est surtout important dans les "vraies applications" des séries de Fourier (style compression JPEG ou autre) et que dans les branches "maths pures", on en parle moins.