Equivalence et nature de séries
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)

-
eratos
- Membre Relatif
- Messages: 280
- Enregistré le: 30 Oct 2009, 13:23
-
 par eratos » 31 Oct 2012, 15:02
par eratos » 31 Oct 2012, 15:02
bonsoir. J'ai un peu de mal avec ces histoires d'équivalence entre fonctions.
On veut étudier la nature de
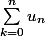
où
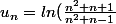)
si je trouve un équivalent de u en l'infini dont la série converge alors c'est gagné. Sauf que je vois pas absolument comment m'y prendre. Je sais que v=
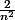
est équivalent de u, mais le montrer, c'est autre chose. Du coup j'essaie au pif avec la définition de u ~v, on a des choses comme (u-v)/v -->0 et u/v -->1. Là, des formes indetérminées naissent et à part un DL en l'infini ( :zen: ), point d'idées me viennent.
La décomposition du ln peut être?
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 31 Oct 2012, 15:09
par arnaud32 » 31 Oct 2012, 15:09
je suppose que c'est
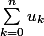
où
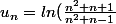)
notes que:
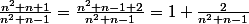
et ln(1+x) = x+o(x) au voisinage de 0

-
raito123
- Habitué(e)
- Messages: 2102
- Enregistré le: 04 Nov 2007, 02:29
-
 par raito123 » 31 Oct 2012, 15:11
par raito123 » 31 Oct 2012, 15:11
Tu sais bien que ln(1+x)=x+o(x) au voisinage de 0 donc ln(1+x) est bien équivalent à x au voisinage de 0 et ben tu appliques directement ce résultat en rajoutant et retranchant 1 pour avoir
))
Les multiples ne doivent pas être utilisés sans nécessité

-
eratos
- Membre Relatif
- Messages: 280
- Enregistré le: 30 Oct 2009, 13:23
-
 par eratos » 31 Oct 2012, 15:15
par eratos » 31 Oct 2012, 15:15
ah ouais bien vu, merci :lol3:

-
eratos
- Membre Relatif
- Messages: 280
- Enregistré le: 30 Oct 2009, 13:23
-
 par eratos » 04 Nov 2012, 12:41
par eratos » 04 Nov 2012, 12:41
eratos a écrit:ah ouais bien vu, merci :lol3:
un autre: a est un réel.
nature de la série de terme général
^{\frac{1}{3}}-(n^2+3)^{\frac{1}{2}})
on obtient
^{\frac{1}{3}}-n(1+\frac{3}{n^2})^{\frac{1}{2}})
puis avec un DL:
])
D'où:
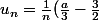+o(\frac{1}{n^2}))
La série converge au cas où a=9/2 car

=o(1/n^2) dans ce cas (et o(1/n) autrement donc la série est divergente).

-
raito123
- Habitué(e)
- Messages: 2102
- Enregistré le: 04 Nov 2007, 02:29
-
 par raito123 » 04 Nov 2012, 12:57
par raito123 » 04 Nov 2012, 12:57
Exact, la série converge si et seulement si a=9/2.
Les multiples ne doivent pas être utilisés sans nécessité

-
eratos
- Membre Relatif
- Messages: 280
- Enregistré le: 30 Oct 2009, 13:23
-
 par eratos » 06 Nov 2012, 22:06
par eratos » 06 Nov 2012, 22:06
Re: :lol3:
Nature des séries:
Peut-on user le théorème des séries altérnées (on a une suite qui en valeur absolue décroit vers 0, alors la série converge)?
}{ln n})
on remarque
^n cos(\pi)}{ln n})
donc la sutie est alternée, en valeur absolue, la suite décroit et converge vers 0. on conclut...
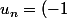^n tg(\frac{1}{n}))
?
Je pense pas, la série est alternée,
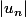
converge vers 0, le point un peu délicat et de montrer la décroissance.
J'ai dérivé pour voir un peu, u(n) croit à gauche de 0 et décroit à droite...(si je me suis pas planté)
-
Le_chat
- Membre Rationnel
- Messages: 938
- Enregistré le: 10 Juin 2009, 12:59
-
 par Le_chat » 07 Nov 2012, 00:40
par Le_chat » 07 Nov 2012, 00:40
Salut.
eratos a écrit:un autre: a est un réel.
nature de la série de terme général
^{\frac{1}{3}}-(n^2+3)^{\frac{1}{2}})
on obtient
^{\frac{1}{3}}-n(1+\frac{3}{n^2})^{\frac{1}{2}})
puis avec un DL:
])
D'où:
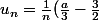+o(\frac{1}{n^2}))
La série converge au cas où a=9/2 car

=o(1/n^2) dans ce cas (et o(1/n) autrement donc la série est divergente).
Pour ceci déjà, le dernier argument est un peu bancal, c'est pas parce que un=o(1/n) que la somme des un ne converge pas.
On peut par exemple dire que si a est différent de 9/2, alors (un) est équivalent à un truc fois 1/n, donc la somme diverge car c'est de signe constant (l'hypothèse signe constant est super importante).
Concernant l'autre exo, petite erreur, c'est un=(-1)^n/ln(n). C'est bien alterné, ça tend vers 0, il te reste à montrer que la suite ( |un| ) décroit, ce qui vrai car (ln(n)) est croissante.

-
eratos
- Membre Relatif
- Messages: 280
- Enregistré le: 30 Oct 2009, 13:23
-
 par eratos » 20 Déc 2012, 20:57
par eratos » 20 Déc 2012, 20:57
salut les matheux en herbes: besoin juste de confirmations.
(je peux développer si besoin)
1/n(n+1) converge bien vers 1?
et du coup 1/n(n+k) (k dans N-{0}) converge vers 1/k
Edit: merci le-chat et les autres, je savais que j'avais oublié un truc :lol3: .
-
Le_chat
- Membre Rationnel
- Messages: 938
- Enregistré le: 10 Juin 2009, 12:59
-
 par Le_chat » 20 Déc 2012, 21:01
par Le_chat » 20 Déc 2012, 21:01
Non ça tend vers 0?

-
eratos
- Membre Relatif
- Messages: 280
- Enregistré le: 30 Oct 2009, 13:23
-
 par eratos » 20 Déc 2012, 21:02
par eratos » 20 Déc 2012, 21:02
arf;.. je veux dire la série de terme général blabla :marteau:
-
Le_chat
- Membre Rationnel
- Messages: 938
- Enregistré le: 10 Juin 2009, 12:59
-
 par Le_chat » 20 Déc 2012, 21:11
par Le_chat » 20 Déc 2012, 21:11
Pour la somme des 1/n(n+1), c'est bien 1 la limite.
Pour 1/n(n+k), ce n'est pas 1/k.
Pour trouver la limite, on dit:
1/n(n+k)=1/k*(1/n-1/(n+k)), donc:
}=\frac{1}{k}(\sum_{n=1}^{N} \frac{1}{n}-\sum_{n=1}^{N} \frac{1}{n+k}))
Continue!
-
adrien69
- Membre Irrationnel
- Messages: 1899
- Enregistré le: 20 Déc 2012, 12:14
-
 par adrien69 » 20 Déc 2012, 21:20
par adrien69 » 20 Déc 2012, 21:20
1/(n(n+k))=1/k *(1/n - 1/(n+k) )
Donc ta somme n'est plus vraiment télescopique, essaie de regarder la somme partielle S(k+1), tu devrais voir assez facilement quelle sera ta somme.

-
eratos
- Membre Relatif
- Messages: 280
- Enregistré le: 30 Oct 2009, 13:23
-
 par eratos » 20 Déc 2012, 22:03
par eratos » 20 Déc 2012, 22:03
j'ai développé, apparemment il reste les termes en 1/n avec 1<=n<=q plus le reste qui tend vers 0, la somme serait
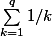
?
-
adrien69
- Membre Irrationnel
- Messages: 1899
- Enregistré le: 20 Déc 2012, 12:14
-
 par adrien69 » 20 Déc 2012, 22:14
par adrien69 » 20 Déc 2012, 22:14
Avec les notations que tu employais au-dessus ce serait plutôt
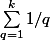
Mais oui, c'est ça.
-
Le_chat
- Membre Rationnel
- Messages: 938
- Enregistré le: 10 Juin 2009, 12:59
-
 par Le_chat » 20 Déc 2012, 22:15
par Le_chat » 20 Déc 2012, 22:15
Sans oublier le facteur 1/k !

-
eratos
- Membre Relatif
- Messages: 280
- Enregistré le: 30 Oct 2009, 13:23
-
 par eratos » 20 Déc 2012, 22:26
par eratos » 20 Déc 2012, 22:26
géniallll!!! :we: merci
Ayé, je suis chaud pour calculer la somme de la série 1/n² :ptdr:

-
eratos
- Membre Relatif
- Messages: 280
- Enregistré le: 30 Oct 2009, 13:23
-
 par eratos » 23 Mar 2013, 11:54
par eratos » 23 Mar 2013, 11:54
La fonction qui fait peur: tangente.
}{1-tan(\frac{1}{n})}))
convergence de la série de terme général

?
j'ai trouvé un équivalent de u_n en l'infini:
}{1-tan(\frac{1}{n})})
Je suis coincé. (va falloir apprendre ses formules trigos :mur: )
-
Le_chat
- Membre Rationnel
- Messages: 938
- Enregistré le: 10 Juin 2009, 12:59
-
 par Le_chat » 23 Mar 2013, 19:45
par Le_chat » 23 Mar 2013, 19:45
Non, pas besoin de trigo! Il suffit de se souvenir que tan(x) équivaut à x en zéro.

-
eratos
- Membre Relatif
- Messages: 280
- Enregistré le: 30 Oct 2009, 13:23
-
 par eratos » 24 Mar 2013, 00:08
par eratos » 24 Mar 2013, 00:08
tan(x)
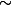
x au voisinage de zéro, ça a l'air intuitif, mais comment le prouver?
est-ce que j'ai le droit de faire ça (un DL à un ordre grossier):
} = \frac{(1+o(x))x}{x+o(x)})
ce qui tend vers 1 quand x tend vers zéro.
Merci encore une fois LeChat :lol3:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 28 invités
=o(1/n^2) dans ce cas (et o(1/n) autrement donc la série est divergente).