Équivalence avec une espérance
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
 par Carlamathsma » 09 Nov 2019, 22:19
par Carlamathsma » 09 Nov 2019, 22:19
Bonjour, j'ai un exercice à faire mais je n'y arrive pas. Est ce que quelqu'un pourrait m'apporter son aide ?
L'énoncé est le suivant :
Soit X une variable aléatoire positive.
1) Montrez que pour tout a>0 on a l'equivalence suivante :
 < \infty \Leftrightarrow \sum_{n\geq 0}^{}{P(X\geq an) < \infty})
Indication : on pourra montrer que
)} \leq E(X) \leq \sum_{n\geq 0}^{}{a(n+1)P(an\leq X <a(n+1))})
Merci d’avance
-
infernaleur
- Membre Irrationnel
- Messages: 1071
- Enregistré le: 20 Avr 2017, 17:45
-
 par infernaleur » 09 Nov 2019, 23:03
par infernaleur » 09 Nov 2019, 23:03
Salut,
comme
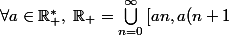[})
,
on a :
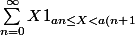} \leq X \leq \sum_{n=0}^{\infty}{X \mathds{1}_{an \leq X < a(n+1)}})
(les séries sont en fait des sommes finies car un nombre infinies d'indicatrices seront nulles donc c'est bien définie)
Ensuite tu as plus qu'à appliquer la croissance et la linéarité de l'espérance.
 par Carlamathsma » 09 Nov 2019, 23:14
par Carlamathsma » 09 Nov 2019, 23:14
Merci pour ta réponse
Je ne vois pas comment faire pour appliquer la croissance et la linéarité a l’espérance
-
infernaleur
- Membre Irrationnel
- Messages: 1071
- Enregistré le: 20 Avr 2017, 17:45
-
 par infernaleur » 09 Nov 2019, 23:17
par infernaleur » 09 Nov 2019, 23:17
}} \leq \sum_{n=0}^{\infty}{X\mathds{1}_{an \leq X < a(n+1)})
Et après tu appliques la croissance et la linéarité de l'espérance
 par Carlamathsma » 10 Nov 2019, 12:10
par Carlamathsma » 10 Nov 2019, 12:10
Je bloque complètement je n’arrive pas à retomber sur le résultat qu’on veux ... pouvez vous m’aider un peu plus s’il vous plaît
-
infernaleur
- Membre Irrationnel
- Messages: 1071
- Enregistré le: 20 Avr 2017, 17:45
-
 par infernaleur » 10 Nov 2019, 13:13
par infernaleur » 10 Nov 2019, 13:13
 par Carlamathsma » 10 Nov 2019, 15:34
par Carlamathsma » 10 Nov 2019, 15:34
Merci et ducoup est ce que je peux écrire que
) = P(X = an))
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 52 invités