Bonjour,
Dans le cadre de mon métier (investisseur) je cherche à résoudre l'équation ci-dessous. Mon inconnue est n
n = P / (E.(1+G)^n)
Merci d'avance pour votre aide!
Louis
Equition avec inconnu en exposant
6 messages
- Page 1 sur 1
Re: Equition avec inconnu en exposant
Bonjour,
Si tu veux une formule, elle fera apparaître la fonction W de Lambert : https://fr.wikipedia.org/wiki/Fonction_W_de_Lambert
Tu ne peux pas avoir de solution au moyen de fonctions élémentaires.
Si tu veux une formule, elle fera apparaître la fonction W de Lambert : https://fr.wikipedia.org/wiki/Fonction_W_de_Lambert
Tu ne peux pas avoir de solution au moyen de fonctions élémentaires.
Re: Equition avec inconnu en exposant
En principe, dans ce genre d'équations, G est petit, par exemple G=0.2 ou G=0.003
Et dans ce cas, par 'tâtonnements' (et les tâtonnements peuvent être très scientifiques), on arrive vite à la solution.
Et dans ce cas, par 'tâtonnements' (et les tâtonnements peuvent être très scientifiques), on arrive vite à la solution.
Re: Equition avec inconnu en exposant
Merci pour vos réponses
Mon objectif est de pouvoir intégrer cette formule dans Excel pour pouvoir déterminer n en modifiant les valeurs de P; E et ; g
En effet g est ici un taux de croissance donc petit.
Encore merci
Louis
Mon objectif est de pouvoir intégrer cette formule dans Excel pour pouvoir déterminer n en modifiant les valeurs de P; E et ; g
En effet g est ici un taux de croissance donc petit.
Encore merci
Louis
Re: Equition avec inconnu en exposant
Bonjour,
Avec G "petit", on peut approcher la valeur de n avec un développement limité.
Si on se limite pour avoir une équation de degré 3, sauf erreur on trouve que n est la solution réelle de :
n³ * G² + n² * (2G + G²) + 2n - 2P/E = 0
Cela ne donnera évidemment qu'une valeur approchée de n
Exemple numérique ;
Si on a :
P = 5
E = 2
G = 0,02
n est "presque" la solution de n³ * G² + n² * (2G + G²) + 2n - 2P/E = 0
soit de : 0,0004n³ + 0,0404n² + 2n - 5 = 0
dont la solution réelle est : n = 2,38262172276...
et en vérifiant en remettant cette valeur dans n = P / (E.(1+G)^n) ...
2,38262172276 =? 5/(2 * (1+0,02)^2,38262172276)
2,38262172276 =? 5/(2 * (1+0,02)^2,38262172276)
2,38262172276 =? 2,38478401839
Presque bon ...
Mais probablement inacceptable dans le domaine de la finance.

Avec G "petit", on peut approcher la valeur de n avec un développement limité.
Si on se limite pour avoir une équation de degré 3, sauf erreur on trouve que n est la solution réelle de :
n³ * G² + n² * (2G + G²) + 2n - 2P/E = 0
Cela ne donnera évidemment qu'une valeur approchée de n
Exemple numérique ;
Si on a :
P = 5
E = 2
G = 0,02
n est "presque" la solution de n³ * G² + n² * (2G + G²) + 2n - 2P/E = 0
soit de : 0,0004n³ + 0,0404n² + 2n - 5 = 0
dont la solution réelle est : n = 2,38262172276...
et en vérifiant en remettant cette valeur dans n = P / (E.(1+G)^n) ...
2,38262172276 =? 5/(2 * (1+0,02)^2,38262172276)
2,38262172276 =? 5/(2 * (1+0,02)^2,38262172276)
2,38262172276 =? 2,38478401839
Presque bon ...
Mais probablement inacceptable dans le domaine de la finance.
Re: Equition avec inconnu en exposant
Dans Excel, tu as un solveur. Tu peux l'utiliser pour résoudre ton équation. Ça ne te convient pas ?
Sinon, j'ai vu qu'il y a des macros pour Excel qui permettent de disposer de la fonction W de Lambert ...
Exemples d'utilisation du solveur dans LibreOffice (le P/E/(1+G) sert de valeur initiale pour la case B2 - on demande au solveur de modifier la case B2 pour obtenir 0 dans la case B8 qui est la différence de B2 et B6) :
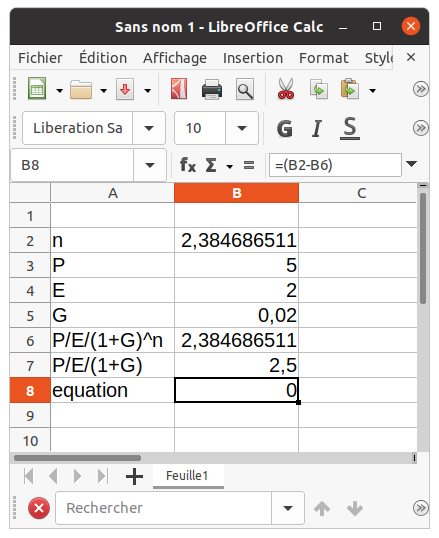
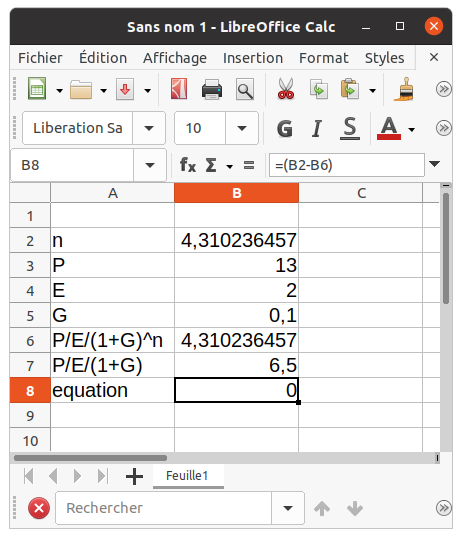
Sinon, j'ai vu qu'il y a des macros pour Excel qui permettent de disposer de la fonction W de Lambert ...
Exemples d'utilisation du solveur dans LibreOffice (le P/E/(1+G) sert de valeur initiale pour la case B2 - on demande au solveur de modifier la case B2 pour obtenir 0 dans la case B8 qui est la différence de B2 et B6) :


6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 71 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
