Un équilibre.

[Lionel144]

Bonjour à tous

J'ai une plaque d'acier connue, qui correspond à un polygone convexe de n sommets. Je la pose sur la pointe d'un clou avec un poids de un kilogramme sur un des sommets. Comment est-ce que je peux calculer le poids de l'ensemble des autres sommets qu'il faudra que je charge afin de réaliser l'équilibre?

Cela fait maintenant longtemps que je cherche et je n'ai pas trouvé un seul exemple où les coefficients braycentriques ne soient pas fournis dans l'énnoncé. Je suis prêt à faire tout le travail, il me manque juste le libellé de la technique qui me permette d'y parvenir.

Je vous remercie par avance.

[Robot]

Le poids de la plaque est négligeable ?
Quelle est au juste ta question ?
Il suffit de charger deux autres sommets de la plaque.

[Lionel144]

Le poids de la plaque est négligeable ?
Quelle est au juste ta question ?
Il suffit de charger deux autres sommets de la plaque.

Merci de m'avoir répondu.

Oui, le poids de la plaque est négligeable.
S'il suffit de charger deux autres sommets, ceux qui restent seront chargés à zéro, pas de problème.
Mais au juste pourquoi deux sommets seulement?
Et puis comment est-ce que je peux calculer ces charges?

La question est simple: Comment calculer les coefficients barycentriques des sommets d'un polygone connu, convexe, pour un quelconque point P connu, situé à l'intérieur de celui-ci?

[Robot]

Etant donné un point P à l'intérieur du polygone, et A étant le sommet déjà chargé, on choisit deux autres sommets B et C tels que P soit à l'intérieur du triangle ABC. On calcule alors les coordonnées barycentrique de P relativement à ABC : trois équations à trois inconnues, et on a tout ce qu'il faut.

[Lionel144]

Etant donné un point P à l'intérieur du polygone, et A étant le sommet déjà chargé, on choisit deux autres sommets B et C tels que P soit à l'intérieur du triangle ABC. On calcule alors les coordonnées barycentrique de P relativement à ABC : trois équations à trois inconnues, et on a tout ce qu'il faut.

Oui, vu sous cet angle, ma question ne se pose même pas.
Je me suis mal exprimé il me semble.
Je n'aurais sûrement pas du dire que la masse du polygone est négligeable. Disons qu'elle est non nulle.
Et si j'ai dit que je charge un premier sommet, c'était pour éviter d'avoir un ensemble infini de solutions.

à la base mon problème est de pouvoir déterminer et calculer les n coefficients de n sommets d'un polygone convexe connu dans un plan, pour qu'un point P(x, y) puis satisfaire la fonction vectorielle de leibniz.

Suivant à cela, la plaque d'acier et les charge sont une représentation matérielle du problème, et je pensais que pas ce biais là, j'aurais pu me faire bien comprendre.

En fait j'y arrive pour trois et quatre sommets, mais pas pour cinq et au-delà.

[Robot]

Faudrait savoir ... négligeable ou pas négligeable ?
Pourrais-tu poser ton problème sans en changer quand j'apporte une réponse ?

Oui, vu sous cet angle, ma question ne se pose même pas.
à la base mon problème est de pouvoir déterminer et calculer les n coefficients de n sommets d'un polygone convexe connu dans un plan, pour qu'un point P(x, y) puis satisfaire la fonction vectorielle de leibniz.

Si je comprend bien, tu veux écrire un point comme barycentre des sommets du polygone, affectés d'un certain poids ? Oui ou non ?
Si le nombre n de sommets est supérieur à 3, il y a une infinité de solutions.
Et je ne vois pas pourquoi la solution que j'ai déjà proposée ne te plait pas. Parmi cette infinité de solutions, il y en a une où seulement trois sommets ont des poids non nuls (et cette solution est alors unique).

[Ben314]

...à la base mon problème est de pouvoir déterminer et calculer les n coefficients de n sommets d'un polygone convexe connu dans un plan, pour qu'un point P(x, y) puis satisfaire la fonction vectorielle de leibniz.

Pour reprendre très exactement la même chose que ce que te dit Robot formulé de façon a peine différente, ton égalité vectorielle équivaut à deux égalités entre réels (Plan=2 coordonnées), donc deux "équations" et si tu as plus de deux inconnues réelles (les poids a mettre sur es sommets sont bien des réels et pas des vecteurs) ça va pas marcher en général (=infinité de solutions)

sinon, QUESTION : Tu dit que "tu sait faire pour 4 sommet". Tu peut un peu détailler, ça permettrait éventuellement de comprendre mieux ce que tu cherche a faire.

[Robot]

En fait, trois équations parce qu'on ajoute celle qui exprime que la somme des poids est égale à 1 pour normaliser (il est clair qu'on peut multiplier tous les poids par un même facteur non nul sans changer le barycentre).

[Ben314]

Perso, j'avais cru comprendre qu'un des poids était déjà donné (1Kg fixé sur un des sommets) donc, y'aura pas franchement à "normaliser" la somme et tu n'aura pas d'autre équation que les deux liées aux deux coordonnées.
Si aucun poids n'était connu, les équations seraient homogènes par rapports aux poids donc on aurait soit une unique solution avec tout les poids nuls, soit une infinité de solution et la condition "somme des poids =1" permettrais de n'en considérer qu'une parmi l'infinité. Mais il me semble bien que ce n'est pas le cas ici vu qu'un des poids est donné.

Évidement, tu peut aussi "oublier" que le poids sur tel sommet est connu de façon a rendre le système plus "harmonieux" ce qui fait une inconnue de plus et donc demande une équation de plus. On peut prendre par exemple "somme des poids = 1", mais on pourrait aussi prendre comme équation supplémentaire "tel poid=1Kg" vu qu'en fait c'est précisément ça qu'on a dans les hypothèses...

[Robot]

La formulation du problème est un peu mouvante. Mais, selon Lionel144

"à la base mon problème est de pouvoir déterminer et calculer les n coefficients de n sommets d'un polygone convexe connu dans un plan, pour qu'un point P(x, y) puis satisfaire la fonction vectorielle de leibniz."

Il est bien connu que dans le plan, un repère affine (permettant de définir des coordonnées barycentriques) est la donnée de trois points non alignés.

[Ben314]

Dans ce cas, o.k., ça veut juste dire qu'on a pas la même "base" : je suis parti comme "base" de son premier post...

[Lionel144]

Oui, le problème véritable est bien exprimé dans le premier post.
Après, le poids de la plaque va conditionner des solutions privilégiées pour les coefficients parmi l'infinité.
Et c'est bien le poids de un kilogramme du premier post qui obligeait la solution unique pour tous les coefficients.
Avec ce poids de un kilogramme, il y aura des poids de plaque qui aboutiront à des impossibilités de solutions.

Maintenant je n'ai pas compris pourquoi Robot introduit un triangle à l'endroit où j'ai n sommets.
Si c'est un choix arbitraire, je ne comprends pas comment il s'opère.

Le premier post est une mise en forme physique du problème.
La version mathématique est le travail pour déterminer les coefficients qui permettent de satisfaire la fonction vectorielle de Leibniz pour un point P

a, b, c, d ... n sont les coefficients de sommets.
A, B, C, D ... N sont les points des sommets.

P(x) = a*A(x) + b*B(x) + c*C(x) + d*D(x) .... + n*N(x)
P(y) = a*A(y) + b*B(y) + c*C(y) + d*D(y) .... + n*N(y)


Avec 4 sommets, voici comment je procède :



- Je calcule l’intersection E de la droite (A,B) et la droite (D,C).
- Je calcule les deux intersections de la droite (E,P) sur la droite (A,D) et la droite (B, C).
- A l’aide de I, je calcule les deux coefficients a et d avec le rapport des longueurs des segments.
a = [I, D] / [A, D]
d = [I, A] / [A, D]

- A l’aide de J, je calcule les deux coefficients b et c avec le rapport des longueurs des segments.
b = [J, C] / [B, C]
c = [J, B] / [B, C]

- A l’aide de P, je calcule les pondérations des coefficients a et d avec le rapport des longueurs des segments [P, J] / [I, J] et les pondérations des coefficients b et c avec le rapport des longueurs des segments [P, I] / [I, J]

Dès lors que j’ai trouvé les quatre coefficients je peux calculer la même position du point P sur un autre polygone avec la fonction de Leibniz.

Cela marche très bien, avec cela j’ai développé un des pôles d’un moteur graphique performant.

Malheureusement je ne parviens pas à faire pareil avec 5 sommets ou plus.

Pour info, voici le code de la fonction SrcQuadBarFlt écrite en C.

typedef struct {
point2D Src[4]; // Le quadrilatère de source.
point2D Dest[4]; // Le quadrilatère de destination.
point2D S; // Un point de la source.
point2D D; // Un point de la destination.
float Coef[4]; // Les quatre coefficients de pondération.
} quadbarflt;

/*
--------------------------------------------------------------------------
- Entre D sort S. 27.03.2011 -
--------------------------------------------------------------------------*/
bool SrcQuadBarFlt (quadbarflt *T, point2D Dest) {
point2D I, II, III;
float f;
bool Status;

// PointCpy(&(T->D), Dest); // Copie le point d'entrée.
Status = IntersectionDD2D(*T->Dest ,*(T->Dest+1), *(T->Dest+2), *(T->Dest+3), &III);
if (Status == false) {
III.x = Dest.x + ((*(T->Dest+1)).x-(*(T->Dest)).x);
III.y = Dest.y + ((*(T->Dest+1)).y-(*(T->Dest)).y);
}
IntersectionDD2D(*T->Dest ,*(T->Dest+3), III, Dest, &I);
IntersectionDD2D(*(T->Dest+1) ,*(T->Dest+2), III, Dest, &II);

*(T->Coef+3) = BaryFlt(*T->Dest, I, *(T->Dest+3));
*T->Coef = 1 - (*(T->Coef+3));
*(T->Coef+2) = BaryFlt(*(T->Dest+1), II, *(T->Dest+2));
*(T->Coef+1) = 1-(*(T->Coef+2));
f = BaryFlt(I, Dest, II);
*(T->Coef+1) *= f; *(T->Coef+2) *= f;
*T->Coef *= 1-f; *(T->Coef+3) *= 1-f;

if (*(T->Coef+2) Coef+3) S.x = (*T->Coef*(*(T->Src)).x) + (*(T->Coef+1)*(*(T->Src+1)).x) + (*(T->Coef+2)*(*(T->Src+2)).x) + (*(T->Coef+3)*(*(T->Src+3)).x);
T->S.y = (*T->Coef*(*(T->Src)).y) + (*(T->Coef+1)*(*(T->Src+1)).y) + (*(T->Coef+2)*(*(T->Src+2)).y) + (*(T->Coef+3)*(*(T->Src+3)).y);
return (true);

} // bool SrcQuadBarFlt (Quadbarflt *T, point2D Dest) {

[Ben314]

Après, le poids de la plaque va conditionner des solutions privilégiées pour les coefficients parmi l'infinité.

Absolument pas.
Que la plaque soit massive ou pas, ça ne change rien au fait que des équations (réelles) tu en a deux et c'est tout (correspondant au fait que l'abscisse et l'ordonnée du centre de gravité doivent être égales a des valeurs prédéfinies) donc si tu veut que le truc se résolve "gentiment", ben des inconnues il t'en faut 2 et c'est tout. Donc, par exemple, tu peut fixer les poids que tu met sur tout les sommets sauf 2 d'entre eux et tu aura pas le choix pour les deux derniers. Évidement, si tu rajoute des contraintes comme par exemple le fait que les poids doivent être positifs, ça te rajoute des inégalités a tes égalités, mais, sauf miracle, ça ne conduira toujours pas à une unique solution avec 2 égalités + des inégalités et 2 inconnues.

Et le truc du triangle dont parlait Robot, c'est pour garantir que la solution trouvée consistera en deux poids positifs et ça résulte du simple fait que le barycentre de (A,a),(B,b),(C,c) est a l'intérieur du triangle (ABC) ssi les réels a,b,c sont de même signe. Si tu accepte des poids négatif, tu t'en fout de cette histoire de triangle et tu peut prend 2 points quelconques parmi les autres sommets.

[Ben314]

Et je comprend absolument pas ce que tu bricole dans tes calculs.
Si tu as points connus et un point lui aussi connu et que tu cherche des coeffs tel que 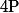soit le barycentre des point pondérés ben ça se traduit évidement par les deux seules équations : épicétout.
Donc si tu veut une unique solution, il faut que tu fixe tout les sauf 2.

Et je comprend absolument pas ce que tu bricole dans le cas de 4 points : le point que tu trouve est éventuellement une solution au problème (j'ai pas vérifié vu la complexité du bidule par rapport à la simplicité de la question), mais je vois nulle part dans ton truc quoi que ce soit qui ressemble à une preuve de l'unicité de ta solution : pourquoi P devrait il être barycentre du I et du J que tu calcule et pas de n'importe quel autre I et J respectivement situés sur (AD) et (BC) et tels que P soit sur (IJ) ?
Sur le dessin tel que tu l'a fait, on pourrait parfaitement prendre I=A (donc pas de poids sur D) et J a l'intersection de (AP) et (BC) et il y a évidement des tas d'autres possibilités pour I.

[Lionel144]

Absolument pas.
Que la plaque soit massive ou pas, ça ne change rien au fait que des équations (réelles) tu en a deux et c'est tout (correspondant au fait que l'abscisse et l'ordonnée du centre de gravité doivent être égales a des valeurs prédéfinies) donc si tu veut que le truc se résolve "gentiment", ben des inconnues il t'en faut 2 et c'est tout.

Que la plaque soit massive ou pas, cela change en ceci, et ce n’est pas ma question principale.

On peut le voir si on considère une balance avec un bras deux fois plus long que l’autre.
Si le bras pèse zéro grammes, Il faudra un poids deux fois plus grand sur le petit côté que sur l’autre.
Si le bras pèse une tonne, ce sera le même système d’équilibre mais il faudra ajouter sur le petit côté une proportion de tonne pour compenser le poids excédentaire du bras le plus long.
Et cela va éliminer des solutions de coefficients dans leur infinité de départ car le poids du bras participe au calcul de l’équilibre, donc des coefficients.
En fait la solution des coefficients dont la somme est égale à un, ne changeront pas. Mais multipliés à des masses réelles il faudra adapter les échelles pour obtenir l’équilibre.

Mais le problème n’est pas là. Le problème est plus simple.

Avec des coefficients on peut calculer un centre de gravité, pourquoi est-ce que l’on ne sais pas où sont écrites les méthodes pour faire le contraire?

Le problème n’est pas à n équations, il y en a bien que deux. Une pour P(x) l’autre pour P(y).
Cramer et le pivot de gauss sont dons hors sujet.

Je connais une méthode qui m’a été donnée pour trois sommets.
Soit le triangle (A, B, C) et la point P quelconque dans ce triangle.
Il faut calculer la surface S du triangle (A, B, C)
Il faut calculer la surface S1 du triangle (P, B, C)
Il faut calculer la surface S2 du triangle (P, A, C)
Il faut calculer la surface S3 du triangle (P, A, B)

a, le coefficient au point A est donné par S1/S.
b, le coefficient au point B est donné par S2/S.
c, le coefficient au point C est donné par S3/S.

Ici j’ai bien trois équations et non pas deux comme dit plus haut !

Mais quels sont les fondements de cette méthode qui me permettraient de l’appliquer à un polygone de n sommets?

Personnellement je suis allé assez loin dans ces explorations là mais à chaque fois je butte dans des paramètres étranges qui me créent des disparités non linéaires et qui apparaissent dont je ne sais où et j’y perds les pédales car je n’ai pas de notions approfondies en mathématiques.

Par exemple avec certaines méthodes géométriques, en excursionnant les polygones j’ai des angles qui fâchent quand les sommets tendent à l’aligner et qui me disent que même si localement je reste convexe, l’ensemble est vu comme concave et j’ai le point P qui sort brusquement.

Alors je pensais que quelqu’un qui sait pourrait m’aider.

Je n’abandonne pas et reste à votre écoute en vous remerciant.

[Lionel144]

Et je comprend absolument pas ce que tu bricole dans tes calculs.
Si tu as points connus et un point lui aussi connu et que tu cherche des coeffs tel que soit le barycentre des point pondérés ben ça se traduit évidement par les deux seules équations : épicétout.

ça oui, je souscris totalement.

[Lionel144]

Donc si tu veut une unique solution, il faut que tu fixe tout les sauf 2.

ça, je ne comprends pas du tout.

C'est quoi "fixer"?

[Lionel144]

Et je comprend absolument pas ce que tu bricole dans le cas de 4 points : le point que tu trouve est éventuellement une solution au problème (j'ai pas vérifié vu la complexité du bidule par rapport à la simplicité de la question), mais je vois nulle part dans ton truc quoi que ce soit qui ressemble à une preuve de l'unicité de ta solution : pourquoi P devrait il être barycentre du I et du J que tu calcule et pas de n'importe quel autre I et J respectivement situés sur (AD) et (BC) et tels que P soit sur (IJ) ?
Sur le dessin tel que tu l'a fait, on pourrait parfaitement prendre I=A (donc pas de poids sur D) et J a l'intersection de (AP) et (BC) et il y a évidement des tas d'autres possibilités pour I.

L'unicité ici, oui je l'obtiens simplement en ayant la somme des coefficients égale à 1.

Oui, il y aurait des tas d'autres possibilités.

Quel est le titre de l'ouvrage où un mathématicien aurait trouvé la meilleure, que je m'y colle?

Que je m'y colle une bonne fois pour toutes avec n sommets!

[Robot]

Alors je pensais que quelqu’un qui sait pourrait m’aider.
Je n’abandonne pas et reste à votre écoute en vous remerciant.

Le problème, c'est que justement tu n'es pas vraiment à l'écoute des gens qui savent ...
Dans le cas du triangle, avec la méthode que tu as décrite et qui est bien connue (les aires des triangles), les coefficients sont bien uniquement déterminés parce qu'on force leur somme à être égale à 1 (ce que je disais plus haut).
A partir de quatre points dans le plan, il n'y a plus unicité des coefficients. Ton calcul te donne un jeu de coefficients qui marchent, mais il y a une infinité d'autres jeux, même si on force la somme des coefficients à être égale à 1, ou même si l'on impose que l'un d'entre eux soit égal à 1.

Je répète un résultat de base du calcul barycentrique : si on a trois points A, B, C non alignés dans le plan, tout autre point du plan s'exprime de manière unique comme barycentre de ces points affectés des poids a, b et c avec a+b+c=1.

Peut-être faudrait-il prendre ta question par un autre bout : pourquoi veut tu exprimer un point du polygone comme barycentre des sommets ? Serait-ce par exemple pour calculer l'image de ce point dans une transformation du polygone (ombre, vue en perspective ... ) ?

[Lionel144]

Le problème, c'est que justement tu n'es pas vraiment à l'écoute des gens qui savent ...

Une leçon d'humilité... Je la prends.