Bonjour,
Cela m'embete un peu de poser la question de facon si direct mais ça fait longtemps que je réfléchis et que rien ne vient...
J'ai un dm à rendre pour demain avec 3 equations fonctionnelles dont les deux premières sont :
f(x+y) = e^x * f(y) + e^y * f(x)
f ' (x) = f(a-x)
La première doit être ramenée à une equation différentielle linéaire simple du premier ordre (analyse) et on doit conclure en synthèse. J'ai dérivé l'expression mais je ne vois pas comment résoudre une équation avec du f ' (x) et du f ' (x+y) ...
La deuxième on doit se ramener à une equation linéaire du 2nd ordre. Les questions nous amènent à montrer que f(x) peut s'écrire f(x) = A sin (x+p) puis a prendre p = Pi/4 - a/2
Je ne sais pas pourquoi mais je n'ai aucune réponse concrète que j'arrive à faire...
Merci d'avance pour votre aide ! :)
Dm equations fonctionnelles
12 messages
- Page 1 sur 1
par Ben314 » 17 Nov 2013, 13:54
Tu n'as aucune hypothèse de plus dans ton énoncé ?
En particulier, au minimum, la continuité de f en 0 pour la première équation ?
Tu as fait comment pour montrer que f était dérivable avant de la dériver ?
En particulier, au minimum, la continuité de f en 0 pour la première équation ?
Tu as fait comment pour montrer que f était dérivable avant de la dériver ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
par Ben314 » 17 Nov 2013, 14:07
En supposant f continue en 0, j'arrive à résoudre la première (mais c'est un peu long...)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
par Ben314 » 17 Nov 2013, 14:44
En supposant f continue en 0, j'arrive à résoudre la première :
Avec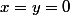
, il vient =0)
=e^xf(h)+e^hf(x))
tend vers +e^0f(x))
(grâce à lhypothèse de continuité de f en 0) c'est à dire vers f(x). Cela prouve que f est continue en tout point x de R.
Ensuite, en prenant x=y, il vient=2e^xf(x))
puis, avec y=2x, =e^{x}f(2x)+e^{2x}f(x)=3e^{2x}f(x))
... (récurence)... =ne^{(n-1)x}f(x))
pour tout n entier positif.
En prenant y=-x il vient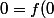=e^xf(-x)+e^{-x}f(x))
donc =-e^{-2x}f(x))
puis =-e^{-2nx}f(nx)=-ne^{(-n-1)x}f(x))
et on en déduit que la formule est valable pour tout entier relatif.
Maintenant, pour tout h assez proche de 0 (mais non nul), on pose=E\big(\frac{1}{h}\big))
(partie entière) : \leq \frac{1}{h}<n(h)+1)
donc h)
tend vers 1 lorsque h tend vers 0. On a alors :
h\Big)=n(h)e^{(n(h)-1)h}f(h))
c'est à dire }{h}=\frac{f\big(n(h)h\Big)}{n(h)h e^{n(h)h-1h}})
qui tend vers }{e})
lorsque h tend vers 0 ce qui prouve que f est dérivable en 0 et que =a)
Enfin, en prenant y=h, on a-f(x)}{h}=\frac{e^{x}f(h)+e^hf(x)-f(x)}{h}=\frac{f(h)}{h}e^x+\frac{e^h-1}{h}f(x)\rightarrow a e^x + f(x))
si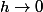 
Ce qui prouve (enfin !!!) que f est dérivable et qu'elle est solution de l'équa.diff.
d'où=(ax+b)e^x)
où 
est une constante quelconque, mais =0\ \Rightarrow\b b=0)
donc f est de la forme =axe^x)
.
On vérifie que=\frac{f(1)}{e}=a)
(donc on peut prendre a quelconque)
Puis qu'une telle fonction f vérifie l'équation fonctionelle de départ.
P.S. Sans l'hypothèse "f continue en 0", je pense qu'il y a des tas d'autres solutions (discontinues en tout points) donc il y a une erreur dans l'énoncé...
Avec
Ensuite, en prenant x=y, il vient
En prenant y=-x il vient
Maintenant, pour tout h assez proche de 0 (mais non nul), on pose
Enfin, en prenant y=h, on a
Ce qui prouve (enfin !!!) que f est dérivable et qu'elle est solution de l'équa.diff.
d'où
On vérifie que
Puis qu'une telle fonction f vérifie l'équation fonctionelle de départ.
P.S. Sans l'hypothèse "f continue en 0", je pense qu'il y a des tas d'autres solutions (discontinues en tout points) donc il y a une erreur dans l'énoncé...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
par Anonyme » 17 Nov 2013, 19:27
Merci à vous !
J'ai réussi à boucler cette première partie ! Je n'ai pas pu me connecter plus tôt sur le forum et oui j'avais bien oublié de dire que f est dérivable sur R désolé..
Mais pour la deuxième partie je cherche la deuxième question : montrer qu'il existe deux réels p et A tels que pour tout c appartenant à R, f(x) = A sin(x+p). J'ai réussi avant à me ramener à une équation différentielle linéaire à coefficients constants avec second membre nul que j'ai résolu et je trouve f(x) = b + ce^-x avec b et c des réels. Mais la je ne vois pas comment arriver à ca.. Je sais tout de même que f(x) = f ' ( a - x)
Merci d'avance et merci pour la partie 1 !
J'ai réussi à boucler cette première partie ! Je n'ai pas pu me connecter plus tôt sur le forum et oui j'avais bien oublié de dire que f est dérivable sur R désolé..
Mais pour la deuxième partie je cherche la deuxième question : montrer qu'il existe deux réels p et A tels que pour tout c appartenant à R, f(x) = A sin(x+p). J'ai réussi avant à me ramener à une équation différentielle linéaire à coefficients constants avec second membre nul que j'ai résolu et je trouve f(x) = b + ce^-x avec b et c des réels. Mais la je ne vois pas comment arriver à ca.. Je sais tout de même que f(x) = f ' ( a - x)
Merci d'avance et merci pour la partie 1 !
par Ben314 » 17 Nov 2013, 20:28
-Anthony- a écrit:Merci à vous !
J'ai réussi à boucler cette première partie ! Je n'ai pas pu me connecter plus tôt sur le forum et oui j'avais bien oublié de dire que f est dérivable sur R désolé..
Mais pour la deuxième partie je cherche la deuxième question : montrer qu'il existe deux réels p et A tels que pour tout c appartenant à R, f(x) = A sin(x+p). J'ai réussi avant à me ramener à une équation différentielle linéaire à coefficients constants avec second membre nul que j'ai résolu et je trouve f(x) = b + ce^-x avec b et c des réels. Mais la je ne vois pas comment arriver à ca.. Je sais tout de même que f(x) = f ' ( a - x)
Merci d'avance et merci pour la partie 1 !
Tu as du te tromper dans les calculs : normalement tu doit arriver à l'équa.diff y"+y=0 au bout de 2 lignes...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
par Ben314 » 17 Nov 2013, 22:11
ça c'est classique (i.e. "à retenir").
Tu considère les coordonnées polaires du point de coordonnées cartésiennes (A,B) : ça signifie qu'il existe
et 
tels que )
et )
(en fait 
)
Ici, comme tu pouvait choisir A et B au pif, ça veut dire que tu peut prendre rho et theta au pif.
Et si tu remplace A et B par les trucs çi dessus, ça va "miraculeusement" se simplifier...
Tu considère les coordonnées polaires du point de coordonnées cartésiennes (A,B) : ça signifie qu'il existe
Ici, comme tu pouvait choisir A et B au pif, ça veut dire que tu peut prendre rho et theta au pif.
Et si tu remplace A et B par les trucs çi dessus, ça va "miraculeusement" se simplifier...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
par Anonyme » 17 Nov 2013, 22:47
Ben314 a écrit:ça c'est classique (i.e. "à retenir").
Tu considère les coordonnées polaires du point de coordonnées cartésiennes (A,B) : ça signifie qu'il existe
Ici, comme tu pouvait choisir A et B au pif, ça veut dire que tu peut prendre rho et theta au pif.
Et si tu remplace A et B par les trucs çi dessus, ça va "miraculeusement" se simplifier...
Merci beaucoup ! Ca m'a permit de terminer cette question !
Pour la suite je ne comprend pas..
par Ben314 » 17 Nov 2013, 23:17
Tu as montré que l'équation f'(x) = f(a-x) impliquait f(x) = A sin(x+p) où A et p sont des constantes arbitraires..
Mais comme tu n'a pas procédé par équivalence tu ne sais pas si la réciproque est vrai (et en fait elle est fausse...) donc on te demande de voir, parmi les fonctions de la forme f(x) = A sin(x+p) lesquelles vérifient effectivement f'(x) = f(a-x)
Mais comme tu n'a pas procédé par équivalence tu ne sais pas si la réciproque est vrai (et en fait elle est fausse...) donc on te demande de voir, parmi les fonctions de la forme f(x) = A sin(x+p) lesquelles vérifient effectivement f'(x) = f(a-x)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 55 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :