Equations différentielles.

[stitch]

bonjour tout le monde,
voila j'ai une petite question :id: :
pourquoi deux solutions distinctes ne peuvent se croiser ?

Sinon, plus généralement, y a t il qqn qui pourait m'indiquer un bon cours(sur internet ou en livre) traitant les eq. diff. ordinaire linéaires, non lin., autonomes ... (cauchy lipsh., Gronwall, etc.)
j'ai un peu de mal avec ce cours en fait :mur: :briques: !
Merci beaucoup pour vos réponses et bonnes soirée!

Stitch

[Nightmare]

Bonsoir,

de quel type d'équation différentielles parles-tu?

[stitch]

salut,
c'est linéaire.

Stitch

[JQ_]

Bonjour,

sans rentrer dans le détail.

Si on considère l'équation différentielle soit une EDO du premier ordre qui relie position, vitesse et temps. Le temps est ici le paramètre d'évolution. est une fonction quelconque (linéaire ou pas) de et de .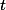
Le théorème de Cauchy-Lipshitz nous garanti, sous certaines conditions sur , l'existence et l'unicité des courbes intégrales (les solutions) restreint éventuellement à des ouverts . Ces courbes sont alors complètements déterminées par une condition initiale : c'est-à-dire la donnée du point . Ceci revient à bien poser le problème de Cauchy.

L'intérêt de la chose : énorme !
Si on revient à l'idée physique d'un système qui évolue au cours du temps. Imaginons qu'à un certain point (moment) la courbe intégrale se divise en plusieurs autres courbes quelle en serait la signification ?
C'est qu'à partir de ce moment le système admet plusieurs futurs possibles. Gênant dans le cadre la mécanique classique, par exemple, qui est complètement déterministe.
Idem, pour deux courbes qui s'interceptent en un point. En ce point on ne peut déterminer ni le passé du système (il y en à deux) ni son futur (deux encore).

Plus simplement cela permet de fixer les limites de validité des solutions (au plus grand ouvert ) et cela sans même avoir à résoudre l'équation.

JQ_

[stitch]

bonjour,
merci JQ_ pour ta réponse, je crois que je saisis mieux maintenant.

Stitch