Equations différentielles ("simple")
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Isendar
- Messages: 7
- Enregistré le: 01 Mai 2008, 08:28
-
 par Isendar » 02 Mai 2008, 09:10
par Isendar » 02 Mai 2008, 09:10
Voici quelques dérivées partielles et j'aimerais savoir de quelle maniere vous vous y seriez pris pour les résoudre.
1)u'= id.u + id
2)u"= -u
3)
)
= g.u (g > ou égal à 0, avec "n" un naturel)
4) u'(t) =
}{u^2(t)})
( u(0)=1 u: I---> [0, infini] )
p.s.: pour le 3) c'est "u" n-fois dérivé
-
JQ_
- Membre Naturel
- Messages: 10
- Enregistré le: 01 Mai 2008, 21:09
-
 par JQ_ » 02 Mai 2008, 10:03
par JQ_ » 02 Mai 2008, 10:03
1) l'écriture laisse à penser que c'est une equa. diff. sur une application ?
2)
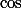
et
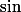
devraient faire l'affaire.
3) pour
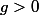
on a
 = \sum_{i=1}^n c_i e^{r_it}$)
où
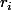
est racine de l'équation
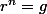
. Pour
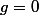
on a un polynôme par intégration directe.
4)
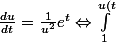} u^2 d u = \int_0^t e^t dt \Leftrightarrow \frac{1}{3}(u^3(t) - 1) = e^t - 1 <br />\Leftrightarrow u(t) = \sqrt[3]{3 e^t - 2})
-
Isendar
- Messages: 7
- Enregistré le: 01 Mai 2008, 08:28
-
 par Isendar » 02 Mai 2008, 10:31
par Isendar » 02 Mai 2008, 10:31
1) oui l'identité renvoie bien a une application
2)j'avais déja pensé a utlisé les cos et sin mais je ne vois pas trop comment démarrer a partir de ca.
4)Lors de ta première integrale, pourquoi la premiere borne est "1" et pas "0" plutôt? et que devient l'exponentiel ?
-
Isendar
- Messages: 7
- Enregistré le: 01 Mai 2008, 08:28
-
 par Isendar » 03 Mai 2008, 09:03
par Isendar » 03 Mai 2008, 09:03
Personne n'a une maniere simple et claire pour résoudre ces differentes équations diferentielles ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 36 invités