Équations différentielle d'Euler

[Xzander]

Bonjour, ça fait quatre heures que j'essaie de passer au travers de cette équation. Voilà, j'ai t²y'' + aty' + by = 0. Je dois prouver que l'on peut la rendre à coefficients constants en procédant au changement de variables x = ln(t). Je commence donc par diviser le tout par t² afin d'obtenir une forme plus conventionnelle:

t²y'' + aty' + by = 0
y'' + at^(-1)y' + bt^(-2)y = 0

Or, il se trouve que
x=ln(t)
dx/dt=1/t
d2x/dt2=-1/t^2

Je peux donc remplacer:
y'' + ay'(dx/dt) - by(d2x/dt2)
d2y/dt2 + a(dy/dt)(dx/dt) - by(d2x/dt2)

C'est à ce point que je bloque. Je crois que mon erreur provient du changement de variable et des dérivées de y par rapport à t. Il y a probablement un concept que je n'applique pas correctement. Merci pour toute idée!

[abcd22]

Bonsoir,
Si on écrit le changement de variable dans l´autre sens : , , , et , et on peut remplacer dans l´équation de départ.

[Xzander]

Merci pour le hint, mais je crois que j'aurais dû préciser que y' et y'' signifient respectivement dy/dt et d2y/dt2. On ne peut donc pas remplacer directement.

Au fait, comment fait-on pour avoir des équations en images comme tu as fait abcd22?

[abcd22]

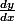Avec ce que j´ai écrit on peut exprimer et en fonction de et .

Pour les formules il faut utiliser le langage LaTeX et les mettre entre balises [ tex] et [ /tex] (sans espaces dans les balises). Tu devrais trouver plusieurs discussions dessus en faisant une recherche sur le forum.

Edit : tu peux aussi voir les codes utilisés en citant un message.