équations aux dérivées partielles

[egan]

Salut,
Je me demandais comment on pouvait faire pour résoudre ça. Je ne vois pas comment faire.

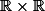
Soit une fonction définie de vérifiant:



Merci d'avance.
@+ Boris.

[Ben314]

Salut,
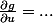
La seule méthode que je connaisse pour les e.d.p, c'est de considérer une fonction avec et choisies de façon à ce que l'équation se réécrive sous la forme (ne dépendant pas de )
Ici,... ça marche.

[Pythales]

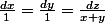
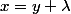
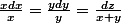
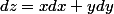
Les caractéristiques te donnent soit et soit ou
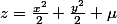
A toi de conclure

[egan]

Pythales, je ne comprends pas ce que tu fais.

[Pythales]

Je ne fais qu'appliquer la théorie des équations aux dérivées partielles linéaires du 1er ordre.
Ce serait trop long à développer ici.

[Ben314]

Moi non plus, mais ça veut juste dire qu'il a plus de bagage que moi (ou que toi ?) concernant les e.d.p. (faut dire que moi de bagage que moi en e.d.p., c'est dur...)
Sinon, si tu veut rester avec du "sans connaissances particulières", tu as regardé la méthode que je te propose (c'est niveau Lycée + epsilon)

[egan]

J'étais en train de voir ce qu'on pouvait faire avec la tienne justement.

[egan]

Je ne vois pas comment construire g en fait.

[Ben314]

Si tu prend alors
Pour que ça "colle" avec ton énoncé, il suffirait que donc, par exemple que et que (il faut que soit bijective pour pouvoir retrouver la fonction une fois que l'on aura trouvé ).

Donc, comme par hasard, posons .
On a donc et ce qui fait que l'équation de départ s'écrit ...

[Pythales]

Pour compléter le message #3, on écrit :
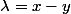
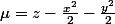
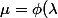et et la solution donne
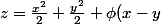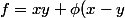Noter que la méthode de Ben314 donne ce qui n'est pas fondamentalement différent puisque la fonction est arbitraire ...