Bonjour à tous.
Nouveau sur ce forum, je me présente rapidement.
Nicolas dans la vie de tous les jours, je suis étudiant dans une école de jeux vidéos et travaille actuellement sur un projet de jeu étudiant que nous développons durant l'été à 8 (dont 2 programmeurs).
Je viens vous voir dans le cadre d'une demande qui va surement vous paraitre un peu originale, mais j'ai besoin de maths pour programmer un jeu vidéo, et plus particulièrement pour gérer les collisions avec le décor durant la partie.
Voici une image tirée d'un prototype du jeu :
http://img79.imageshack.us/img79/1364/screenjeulc2.png
A droite, vous pouvez voir ce que j'appelle le masque de collision (la courbe rouge épaisse).
Lorsque le personnage (le chat humanoide) entre en collision avec cette courbe, il arrête son déplacement.
Ce que nous voulons, c'est de le faire repartir si le déplacement ne passe pas par le masque de collision.
Donc, notre but est de calculer la tangente à la courbe au point de collision, afin de dire au programme : "fait repartir le personnage si la souris se trouve à gauche de la tangente"
J'aurais donc quelques questions...
Premièrement, peut-il exister une équation de courbe pour l'exemple donné ?
Deuxièmement, à quoi ressemblerait-elle ?
Troisièmement, comment la calculer ?
Après si y'a (on sait jamais) des fans de programmation dans le coin, pensez vous qu'il soit capable, en actionscript 2.0, de créer un moteur qui calculerait automatiquement l'équation d'une courbe tracée en vectoriel sous flash CS3 ?..
Merci à tous ceux qui auront pris le temps de me lire !
Equation d'une courbe complexe
10 messages
- Page 1 sur 1
Salut,
- une courbe a toujours une équation (même si on ne sait pas la calculer)
- il me semble que ta courbe ressemble à un morceau d'ellipse.
- donc une équation du style
avec un changement de repère convenable.
- en général (mais pas toujours) les logiciels de dessin vectoriel utilisent des courbes de Bezier. C'est le cas si chaque morceau de courbe a 4 points de contrôle. Dans ce cas l'équation de la courbe est
où A B C et D sont les points de contrôles.
Si on peut récupérer leurs coordonnées il est facile d'avoir l'équation de la courbe et donc celles des tangentes.
Encore que récupérer la valeur deà partir de celles de
et
demande la résolution numérique d'une équation.
nuage a écrit:Salut,
- une courbe a toujours une équation (même si on ne sait pas la calculer)
Déjà un bon point, je pensais que si la courbe avait deux coordonnées y pour un meme x il n'y avait pas d'équation possible.- il me semble que ta courbe ressemble à un morceau d'ellipse.
- donc une équation du style
avec un changement de repère convenable.
Euh pour le coup, je me suis arreté aux maths de Terminale S et j'ai énormément oublié... (pas en faire pendant 2 ans, ça aide pas...)
Du coup, je ne comprends pas ce que tu entends par changement de repère convenable ?
Actuellement l'origine du repère se situe en haut à gauche de l'écran de jeu.- en général (mais pas toujours) les logiciels de dessin vectoriel utilisent des courbes de Bezier. C'est le cas si chaque morceau de courbe a 4 points de contrôle. Dans ce cas l'équation de la courbe est
où A B C et D sont les points de contrôles.
Si on peut récupérer leurs coordonnées il est facile d'avoir l'équation de la courbe et donc celles des tangentes.
Encore que récupérer la valeur deà partir de celles de
et
demande la résolution numérique d'une équation.
Juste une question rapide pour comprendre ça... à quoi correspond le t ? ^^' Sinon ça me semble assez clair, bien que je demande s'ile st possible de récupérer les points de controle. Je ferais des recherches demain.
Un très grand merci à toi pour ta réponse, surtout qu'elle a été particulièrement rapide
Nicolas.
pour le changement de repère :
l'équation que j'ai donnée correspond à une ellipse dont le centre est l'origine du repère (ce qui n'est pas le cas) et dont les axes sont parallèles aux axes du repère (c'est pas le cas non plus) il faut donc déplacer le centre et faire tourner les axes. Il y a des formules pour ça, mais je ne crois pas qu'elles soient intéressantes dans ton cas, qui, je pense, relève plutôt du genre courbe de Bézier.
Pour le dernier point le paramètre fait correspondre à chaque point du segment [0,1] un point de la courbe. L'idée est qu'une courbe est un segment de droite déformé. À chaque point du segment de droite
fait correspondre à chaque point du segment [0,1] un point de la courbe. L'idée est qu'une courbe est un segment de droite déformé. À chaque point du segment de droite  ;
; 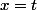
 on fait correspondre un point de la courbe.
on fait correspondre un point de la courbe.
Ps : mes explications sont un peu confuses, si tu as des problèmes pour comprendre ce que j'ai dit n'hésite pas à reposter.
A+
l'équation que j'ai donnée correspond à une ellipse dont le centre est l'origine du repère (ce qui n'est pas le cas) et dont les axes sont parallèles aux axes du repère (c'est pas le cas non plus) il faut donc déplacer le centre et faire tourner les axes. Il y a des formules pour ça, mais je ne crois pas qu'elles soient intéressantes dans ton cas, qui, je pense, relève plutôt du genre courbe de Bézier.
Pour le dernier point le paramètre
Ps : mes explications sont un peu confuses, si tu as des problèmes pour comprendre ce que j'ai dit n'hésite pas à reposter.
A+
nuage a écrit:Salut,
- une courbe a toujours une équation (même si on ne sait pas la calculer)
Salut nuage,
J'avais juste une petite remarque : Il faut faire gaffe à ce que tu dis , une courbe n'a pas toujours d'équation comme tu le dis .
Exemple : Prends un bracelet élastique . Au repos ça te fait un joli cercle ou du moins une ellipse , mais dès que tu commence à le tordre et à faire des nuds de partout, tu obtiendra une courbe mais alors pour en donner une équation ça risque d'être dur...
En revanche on peut peut être espérer avoir une équation locale en un voisinage de chaque point et encore, ce n'est pas gagné .
Salut,
Il est souvent difficile, voir inutile, de chercher une équation pour une courbe donnée.
Ça ne l'empêche pas d'exister.
Par exemple dans le cas de l'élastique emmêlé (disons d'une arête de l'élastique) on a une courbe dont on peut penser qu'elle est de classe C-infini.
On peut donc la paramétrer par son abscisse curviligne.
Ceci étant, je fait parfois attention à ce que je dit (pas toujours malheureusement !).
C'est pourquoi j'avais précisé même si on ne sait pas la calculer
Daniel-Jackson a écrit:Salut nuage,
J'avais juste une petite remarque : Il faut faire gaffe à ce que tu dis , une courbe n'a pas toujours d'équation comme tu le dis .
Exemple : Prends un bracelet élastique . Au repos ça te fait un joli cercle ou du moins une ellipse , mais dès que tu commence à le tordre et à faire des nuds de partout, tu obtiendra une courbe mais alors pour en donner une équation ça risque d'être dur...
En revanche on peut peut être espérer avoir une équation locale en un voisinage de chaque point et encore, ce n'est pas gagné .
Il est souvent difficile, voir inutile, de chercher une équation pour une courbe donnée.
Ça ne l'empêche pas d'exister.
Par exemple dans le cas de l'élastique emmêlé (disons d'une arête de l'élastique) on a une courbe dont on peut penser qu'elle est de classe C-infini.
On peut donc la paramétrer par son abscisse curviligne.
Ceci étant, je fait parfois attention à ce que je dit (pas toujours malheureusement !).
C'est pourquoi j'avais précisé même si on ne sait pas la calculer
Bon pour information, cette équation étant impossible à calculer à l'aide du logiciel de programmation utilisé, on a choisi de changer de système de déplacement, et donc d'abandonner l'analogique... On a viré sur un déplacement du personnage à 16 directions, et donc par conséquent nous n'avons plus besoin de ces calculs (trop ?) complexes. ^^
Je tiens quand meme à remercier encore nuage pour sa réponse très rapide, bonne continuation pour ce forum très bien pensé !
(J'aurais du le découvrir quand j'étais en TS, ça m'aurait évité un 8 au BAC :D)
Je tiens quand meme à remercier encore nuage pour sa réponse très rapide, bonne continuation pour ce forum très bien pensé !
(J'aurais du le découvrir quand j'étais en TS, ça m'aurait évité un 8 au BAC :D)
nuage a écrit:Salut,
Il est souvent difficile, voir inutile, de chercher une équation pour une courbe donnée.
Ça ne l'empêche pas d'exister.
Par exemple dans le cas de l'élastique emmêlé (disons d'une arête de l'élastique) on a une courbe dont on peut penser qu'elle est de classe C-infini.
On peut donc la paramétrer par son abscisse curviligne.
Ceci étant, je fait parfois attention à ce que je dit (pas toujours malheureusement !).
C'est pourquoi j'avais précisé même si on ne sait pas la calculer
Ah oui mais attention on peu très vite gâter les choses. En créant de singularité de partout c'est à dire des point "anguleux" où la courbe n'est pas "lisse" donc exclure toute chance qu'elle soit de classe C-infini. si on élargit la définition d'une courbe comme étant un objet de "dimension" 1 , en d'autre terme un objet aussi "gros" qu'une droite, complexe ou réelle selon le cas. Par exemple n'importe que ouvert de C (le plan complexe) est une courbe complexe , alors que c'est une surface réelle... et je serai étonné que tu puisse me donner une équation à des ouverts bien tordus de C .
Et puis pour l'abscisse curviligne , je serai bien curieux de savoir comment tu fais ça. Parce que tu dis qu'on considère l'abscisse curviligne sans savoir sa forme ...enfin c'est confus tout ça pour moi
donc j'insiste : On ne peut pas toujours donner une équation à une courbe
Salut,
soit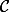 un sous-ensemble de
un sous-ensemble de  .
.
Une équation de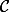 :
: =1)
D'accord ça ne présente aucun intérêt, mais c'est une équation de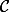 .
.
Tu peux voir, pour mon avis sur la question, le message #13 de cette discussion
[modification]
Je m'excuse d'avoir trop vite lu ton message (je ne fait pas toujours attention à ce que j'écris)
Je suis pleinement d'accord avec la proposition :
On ne peut peut pas toujours donner une équation intéressante d'une courbe.
Ce qui n'empêche nullement l'existence d'équations de la courbe.
soit
Une équation de
D'accord ça ne présente aucun intérêt, mais c'est une équation de
Tu peux voir, pour mon avis sur la question, le message #13 de cette discussion
[modification]
Je m'excuse d'avoir trop vite lu ton message (je ne fait pas toujours attention à ce que j'écris)
Je suis pleinement d'accord avec la proposition :
On ne peut peut pas toujours donner une équation intéressante d'une courbe.
Ce qui n'empêche nullement l'existence d'équations de la courbe.
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 48 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
