Equation de trigo

par **martin34170** » 12 Sep 2010, 11:38

Bonjour, je commence une année de ptsi, le premier DM est un peu délicat.
Il y a une équation trigonométrique que je n'arrive pas à résoudre...

Il faut résoudre dans

l'équation suivante :

J'ai commencé par mettre au même dénominateur pour le membre de gauche mais après je suis bloqué...
Pourriez-vous m'aider ?
Merci d'avance

par **Purrace** » 12 Sep 2010, 11:50

faut jamais aller a la bourrin dans ce genre dexo faut que tu trafique un peu pour trouver des forme sympa

par **Buggy94** » 12 Sep 2010, 11:55

Développe le membre de droite ( cos(a-b) = cos(a)cos(b) - sin(a)sin(b) ), passe le à gauche, factorise et regarde ce que ça fait :+:

par **remixi** » 12 Sep 2010, 13:24

Le problème viens avec le sin(2x)

par **martin34170** » 12 Sep 2010, 13:40

Oui avec la formule sin2x=2*sinx*cosx mais, ensuite j'ai un souci de factorisation...
J'arrive à ça :

Pourriez-vous m'indiquer l'étape suivante ?
Merci d'avance

par **martin34170** » 12 Sep 2010, 15:39

Up un peu d'aide s'il vous plait :)

par **Sa Majesté** » 12 Sep 2010, 15:49

Simplifie en multipliant par

par **Purrace** » 12 Sep 2010, 15:57

regarde ce que fait cos(pi/4-x) en fonction de sinx +cosx

par **martin34170** » 12 Sep 2010, 16:30

En simplifiant, j'arrive à

Je ne vois pas la suite, pouvez-vous me l'indiquer ?

Merci d'avance

par **Sa Majesté** » 12 Sep 2010, 16:36

Ensuite ça fait

Et là c'est gagné car on sait résoudre cos(a)=cos(b) isn't it ?

par **martin34170** » 12 Sep 2010, 18:22

Oui, ca fait

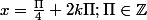
Merci Beaucoup

par **Sa Majesté** » 12 Sep 2010, 18:23

Non pas tout à fait

par **mathelot** » 13 Sep 2010, 06:20

martin34170 a écrit:Il y a une équation trigonométrique que je n'arrive pas à résoudre...

cette identité est bien connue:

et

sont inverses:

Equation de trigo

equation de trigo

Qui est en ligne