Équation
18 messages
- Page 1 sur 1
Équation
Bonjour, j'ai la rentrée de prépa la semaine prochaine et j'ai des équations a faire et j'ai un peu de mal ^^'
Voici une des équations :
3x^3+3x^2+3x+1=0
Quelqu'un peut il m'aider ?
Voici une des équations :
3x^3+3x^2+3x+1=0
Quelqu'un peut il m'aider ?
Elay0r a écrit:Bonjour, j'ai la rentrée de prépa la semaine prochaine et j'ai des équations a faire et j'ai un peu de mal ^^'
Voici une des équations :
3x^3+3x^2+3x+1=0
Quelqu'un peut il m'aider ?
Bonjour,
Ce polynôme ressemble à quelque chose de très connu....
On peut , de ce fait, le factoriser à vue...
je l'ai factorisé j'ai obtenu 2x^3 + (x+1) = 0 je trouve donc x= -1/(1+2^(1/3))
Mais pour un polynôme de 3ème degrés il faut en principe trouvé trois racines du coup j'ai essayé de factorisé mon polynôme par (x+1/(1+2^(1/3)) pour obtenir un un polynôme du second degrés et trouver les deux racines manquantes mais ça ne me donne rien...du coup j'ai essayé une autre technique j'ai trouvé mon polynôme en bricolant un peu mais du coup quand je fais mon discriminant il est négatif... je n'aurais donc qu'une solution celle du début... mais tout ça ne me parait pas très juste...
HELP !
Mais pour un polynôme de 3ème degrés il faut en principe trouvé trois racines du coup j'ai essayé de factorisé mon polynôme par (x+1/(1+2^(1/3)) pour obtenir un un polynôme du second degrés et trouver les deux racines manquantes mais ça ne me donne rien...du coup j'ai essayé une autre technique j'ai trouvé mon polynôme en bricolant un peu mais du coup quand je fais mon discriminant il est négatif... je n'aurais donc qu'une solution celle du début... mais tout ça ne me parait pas très juste...
HELP !
1) Quel est le domaine de définition de ta fonction f(x) telle que l'égalité s'écrive f(x) = 0 ?
2) Tu met l'expression au carré mais attention : le carré de la somme n'est pas la somme des carrés !
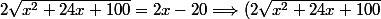^2 = (2x - 20)^2) Tu auras un polynôme du second degré. Tu regarde ces racines.
Tu auras un polynôme du second degré. Tu regarde ces racines.
3) Comme on a utilisé un raisonnement un implication et pas en équivalence, tu dois vérifié si toutes les solutions trouvées sont solutions du problème.
2) Tu met l'expression au carré mais attention : le carré de la somme n'est pas la somme des carrés !
3) Comme on a utilisé un raisonnement un implication et pas en équivalence, tu dois vérifié si toutes les solutions trouvées sont solutions du problème.
Elay0r a écrit:je trouve x=0 mais si on remplace dans l'équation de départ qui est racine( x+4) + racine(x+20) = 2*racine(x+1) et ben ca ne marche pas
Donc que peux tu dire de l'ensemble des solutions ?
Euh l'equation dont tu parle n'est pas la bonne ?!
Ce ne serais pas plutôt :
EDIT : bug de LATEX : -2x + 20 + 2 V(x^2+24x+100)
bonjour, j'ai de nouveau un problème d'équation ^^'...
Voici mon équation d'origine 3x^2-3x-4V(x^2-x+3)=6, alors voila j'ai tout mis au carré pour me débarrasser de la racine j'obtient 9x^4-18x^3-61x^2-46=0 et je suis bloquée, je pensais factoriser par x^2 mais après j'ai 46/x^2 qui me dérange
Que faire ?
Voici mon équation d'origine 3x^2-3x-4V(x^2-x+3)=6, alors voila j'ai tout mis au carré pour me débarrasser de la racine j'obtient 9x^4-18x^3-61x^2-46=0 et je suis bloquée, je pensais factoriser par x^2 mais après j'ai 46/x^2 qui me dérange
Que faire ?
18 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 62 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
