équation du second degres + racine
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
haydenstrauss
- Membre Relatif
- Messages: 378
- Enregistré le: 11 Juil 2006, 10:19
-
 par haydenstrauss » 07 Sep 2006, 12:48
par haydenstrauss » 07 Sep 2006, 12:48
Bonjour tout le monde.
Comment résoudre une équation du style :
3$ ax^2+bx+c+d\sqrt{x}=0
Merci tout le monde :)
-
Clembou
- Membre Complexe
- Messages: 2732
- Enregistré le: 03 Aoû 2006, 11:00
-
 par Clembou » 07 Sep 2006, 12:51
par Clembou » 07 Sep 2006, 12:51
Je me demande si en multiplant par x de chaque côté on retrouve pas une équation du troisième degré.
Je vais vérifier
 Edit
Edit : Vu le message suivant, :briques:
-
haydenstrauss
- Membre Relatif
- Messages: 378
- Enregistré le: 11 Juil 2006, 10:19
-
 par haydenstrauss » 07 Sep 2006, 12:53
par haydenstrauss » 07 Sep 2006, 12:53
si on multpilie par x de chaque coté sa donne :
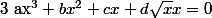
donc
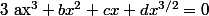
-
nox
- Membre Complexe
- Messages: 2157
- Enregistré le: 14 Juin 2006, 09:32
-
 par nox » 07 Sep 2006, 12:53
par nox » 07 Sep 2006, 12:53
la belle affaire ^^
la racine de x ne disparaitra pas de toute facon
-
nox
- Membre Complexe
- Messages: 2157
- Enregistré le: 14 Juin 2006, 09:32
-
 par nox » 07 Sep 2006, 12:55
par nox » 07 Sep 2006, 12:55
je ne pense pas qu'il y ait une méthode générale...
c'est quoi l'équation exacte ?
tu peux peut-être poser X = racine de x et factoriser le polynôme de degré 4 en bricolant...
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 07 Sep 2006, 12:55
par Flodelarab » 07 Sep 2006, 12:55
tu poses
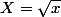
-
nox
- Membre Complexe
- Messages: 2157
- Enregistré le: 14 Juin 2006, 09:32
-
 par nox » 07 Sep 2006, 12:56
par nox » 07 Sep 2006, 12:56
Flodelarab a écrit:tu poses
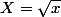
Yeah post croisé :++:
-
haydenstrauss
- Membre Relatif
- Messages: 378
- Enregistré le: 11 Juil 2006, 10:19
-
 par haydenstrauss » 07 Sep 2006, 12:59
par haydenstrauss » 07 Sep 2006, 12:59
sa donnerais :
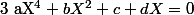
que je ne sais pas résoudre non plus

-
nox
- Membre Complexe
- Messages: 2157
- Enregistré le: 14 Juin 2006, 09:32
-
 par nox » 07 Sep 2006, 13:01
par nox » 07 Sep 2006, 13:01
ba je dirais
nox a écrit:je ne pense pas qu'il y ait une méthode générale...
c'est quoi l'équation exacte ?
tu peux peut-être poser X = racine de x et factoriser le polynôme de degré 4 en bricolant...
-
haydenstrauss
- Membre Relatif
- Messages: 378
- Enregistré le: 11 Juil 2006, 10:19
-
 par haydenstrauss » 07 Sep 2006, 13:03
par haydenstrauss » 07 Sep 2006, 13:03
arf moi qui pensais que j'vais une méthode pour résoudre touw les polynomes :(
-
haydenstrauss
- Membre Relatif
- Messages: 378
- Enregistré le: 11 Juil 2006, 10:19
-
 par haydenstrauss » 07 Sep 2006, 13:04
par haydenstrauss » 07 Sep 2006, 13:04
haa genial je vais regarder sa :)
enfin faudrai deja que je comprene comment resoudre une équation du troisieme degres je trouve la méthode de cardan fastideuse
-
nox
- Membre Complexe
- Messages: 2157
- Enregistré le: 14 Juin 2006, 09:32
-
 par nox » 07 Sep 2006, 13:05
par nox » 07 Sep 2006, 13:05
haydenstrauss a écrit:enfin faudrai deja que je comprene comment resoudre une équation du troisieme degres je trouve la méthode de cardan fastideuse
tu veux pas 100 balles et un mars aussi ? :ptdr:
si tu veux tu peux tjs appliquer la méthode du discriminant pour le degré trois la formule est rigolote :ptdr:
-
haydenstrauss
- Membre Relatif
- Messages: 378
- Enregistré le: 11 Juil 2006, 10:19
-
 par haydenstrauss » 07 Sep 2006, 13:06
par haydenstrauss » 07 Sep 2006, 13:06
si tu l'as ej veux bien la voir :)
-
nox
- Membre Complexe
- Messages: 2157
- Enregistré le: 14 Juin 2006, 09:32
-
 par nox » 07 Sep 2006, 13:08
par nox » 07 Sep 2006, 13:08
c'était ironique...c'est une formule horrible et inutilisable
-
haydenstrauss
- Membre Relatif
- Messages: 378
- Enregistré le: 11 Juil 2006, 10:19
-
 par haydenstrauss » 07 Sep 2006, 13:09
par haydenstrauss » 07 Sep 2006, 13:09
ha ok :p
enfin pas cool de resoudre ses equation premier degres et deuxieme sont simple et tout de suite apres sa devient super compliquer et surtout super fastideux
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 07 Sep 2006, 13:10
par Flodelarab » 07 Sep 2006, 13:10
T un sportif !!!
trace ton polynome a la calculette, puis tu vois bien ou ça coupe l'axe des x....
-
haydenstrauss
- Membre Relatif
- Messages: 378
- Enregistré le: 11 Juil 2006, 10:19
-
 par haydenstrauss » 07 Sep 2006, 13:12
par haydenstrauss » 07 Sep 2006, 13:12
on a pas de tel équation dans le superieur ?
-
nox
- Membre Complexe
- Messages: 2157
- Enregistré le: 14 Juin 2006, 09:32
-
 par nox » 07 Sep 2006, 13:13
par nox » 07 Sep 2006, 13:13
si mais si y'a pas d'astuce on les résoud rarement analytiquement...ou alors avec des détours genre par le matriciel (enfin d'après mon expérience).
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 85 invités
