Equation du second degrès complexe

[suricate0109]

Bonjour!!
J'ai cette équation à resoudre : 5*z^2+3*z*conjugué de z+20i=0

J'ai essayé la méthode avec les racines carrées mais cela ne va pas du tout à cause du conjugué de z, je e vois pas dut tout comment faire

[Rdvn]

Bonjour
Est ce bien 5.z^2+3.zz'+20i=0 (où z' désigne le conjugué de z et . la multiplication) ?
Si oui il y a la méthode ordinaire : z=x+yi, x et y réels, puis un complexe est nul si et ssi ...
Bon courage
Rdvn

[suricate0109]

oui et je trouve 5(x^2+2ixy-y)+3(x^2+y^2)+20i=0 et à partir de là je suis bloquée

[hdci]

oui et je trouve 5(x^2+2ixy-y)+3(x^2+y^2)+20i=0 et à partir de là je suis bloquée

La formule trouvée ne me semble pas correcte : il doit manquer le carré sur le y dans le développement de

Ensuite, que peut-on dire des parties réelles et imaginaires d'un complexe nul ?

Par suite, ne faut-il pas regrouper toutes le parties réelles ensembles et toutes les parties imaginaires ensembles ?

[suricate0109]

J'ai utilisé une identité remarquable (x+iy)^2 =x^2+2ixy-y

La partie réelles est aussi nul?

[hdci]

J'ai utilisé une identité remarquable (x+iy)^2 =x^2+2ixy-y

Il y a toujours une erreur :
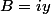
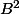
Et si , que vaut ?

La partie réelles est aussi nul?

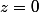
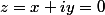
Si avec , que peut-on dire de et de ... ?

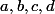
Plus généralement, si sont des réels, que peut-on dire si ?
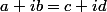
(Une autre façon de poser la question : l'écriture en parties réelle et imaginaire est-elle unique ?)
(Une dernière façon de "voir" : en considérant le point de coordonnées , le point peut-il avoir d'autres coordonnées dans le même repère ?)

[Rdvn]

Re-bonjour
(iy)^2=iy.iy=i^2.y^2=-y^2, et non -y,
après cela, revoie la réponse de hdci : si cela ne t'apparait pas évident, c'est que de grosses révisions s'imposent, niveau Terminale.
Bon courage