Equation fonctionnelle

[lirabo]

Bonjour,

Petite curiosité : l'équation fonctionnelle

On est tenté de montrer que sa solution est
En posant f(1)=k, et en écrivant l'équation pour x=y=1, on trouve puis progressivement en prenant remplaçant x et y par des valeurs sur lesquelles on connait la valeur de f, on montre que f vaut bien pour une infinité de valeur (je pense tout ce qui s'écrit sous la forme (avec n et p entiers)).
Mais, si on ne fait pas l'hypothèse de continuité de f, je n'arrive pas à prouver le résultat pour un x arbitraire (par exemple ) Ma méthode de propagation des valeurs connus de f par application récursive de l'équation fonctionnelle ne permet pas de sortir d'un ensemble de réels. J'aurais la même chose en partant de x=y=pi mais avec un k potentiellement différent.

D'après-vous peut on prouver que les solutions de f sont bien de la forme ou alors peut-on trouver des f "bizarres" qui aurait des formes différentes suivant des ensemble de réels différents ?

[girdav]

Si on remplace et par (a priori aucune hypothèse ne l'interdit) on a donc puis on prend quelconque et et on a donc est impaire ce qui montre en particulier que la solution que tu donnes ne marche pas.

[lirabo]

Si on remplace et par (a priori aucune hypothèse ne l'interdit) on a donc puis on prend quelconque et et on a donc est impaire ce qui montre en particulier que la solution que tu donnes ne marche pas.

Oups désolé : l'équation fonctionnelle c'est

[windows7]

par exemple dans IR +

tu prend f= k*x²*1I_q

bon si x et y dans Q pas de pb
si x dans Q et y non

on aurait f(x)+f(y)= f(racine(x²+y²)) = f(x)
or dans IR racine de x²+y² serait irrationel
donc f(V(x²+y²))=0

[ffpower]

Si on pose pour x positif, ton equation devient g(x)+g(y)=g(x+y). Or cette équation a des solutions continues nulle part donc la tienne aussi..

[Djmaxgamer]

Si on pose pour x positif, ton equation devient g(x)+g(y)=g(x+y). Or cette équation a des solutions continues nulle part donc la tienne aussi..

L'équation ne deviendrait-elle pas :
?

[ffpower]

plutot g(x²)+g(y²)=g(x²+y²)

[Djmaxgamer]

plutot g(x²)+g(y²)=g(x²+y²)

Oui pardon, et donc ca revient au même. Désolé :we:

[lirabo]

Si on pose pour x positif, ton equation devient g(x)+g(y)=g(x+y). Or cette équation a des solutions continues nulle part donc la tienne aussi..

Si, ça a l'air correct. Et c'est fort ça...
je pensais que cette éq fonc sur g aurait suffit à prouver la linéarité de g.

tu as des réf sur la démo qui prouve l'existence de telles fonctions continues nulle part et vérifiant l'équation fonctionnelle sur g ?

[ffpower]

La demo est on va dire plutot simple mais utilise le lemme de Zorn, qui lui ne se voit en cours qu'a bac+3 en général. Mais formellement l'idée est la suivante :
-R est un Q-espace vectoriel
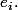
-On peut trouver une base de R en tant que Q-espace vectoriel (base nécessairement infinie ), c'est à dire une famille de réels telle que tout réel s'écrit de maniere unique comme combinaison linéaire finie à coefficients dans Q des C'est pour montrer l'existence de cette base qu'on utilise le lemme de Zorn, on peut donc dire que c'est la partie dure de la demo. Mais intuitivement, l'existence de cette base se montre comme en dimension finie : si on a une famille libre qui n'est pas une base, on peut rajouter un élément de sorte que la famille reste libre. Et Zorn dit qu'a force de rajouter des éléments, au bout d'un nombre infini d'étapes on va finir par tomber sur une base..
-Comme pour les espaces vectoriels de dim finie, on peut définir une application Q-linéaire sur R en définissant ses valeurs sur notre base . Et une application Q-linéaire vérifie en particulier f(x+y)=f(x)+f(y) ( en fait cette équation est même équivalente à la Q-linéarité )
-On peut donc ainsi définir des applications Q-linéaire, en choisissant ses valeurs sur la base. On en définit une telle f de sorte à s'assurer qu'elle n'est pas de la forme f(x)=ax ( par exemple on construit f de sorte qu'elle valle 1 sur tous les )
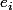
-On a ainsi une f qui vérifie l'équation f(x+y)=f(x)+f(y), et qui ne peut etre continue nulle part, car si elle était continue quelque part, elle le serait partout et serait donc de la forme f(x)=ax

Pour plus de détails, une googlisation sur "equation de Cauchy" ou "base de Hamel" devrait probablement donner des trucs..