équation fonctionnelle CAPES

[fabiench]

Je cherche à démontrer le résultat suivant:

Si f vérifie l'équation fonctionnelle
f(x+y)=f(x)+f(y) et f est continue en un point (par exemple en 0) alors f est continue en tout point x


Merci pour la réponse

[khivapia]

L'équation fonctionnelle permet de montrer que pour tout réel et rationnel.

(on peut le montrer pour les entiers facilement vu la forme de l'équation fonctionnelle, poru les inverses des entiers non nuls en écrivant et l'extension aux rationnels ne pose pas de difficulté en les écrivant comme quotient de deux entiers).


Avec l'équation , on en déduit que est un endomorphisme de 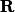considéré comme espace vectoriel sur .

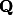On utilise alors le théorème suivant sur les applications linéaires continues : "Soit linéaire de dans espaces vectoriels normés sur 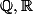ou . Alors est continue si et seulement si est continue en 0 (si et seulement si est bornée sur la boule unité ou la sphère unité, etc.)."

D'où le résultat.

Si elle n'est pas continue en 0, on s'y ramène...

[khivapia]

En fait c'est un peu trop fort, on doit avoir un moyen de tout faire avec les epsilon et les alphas en utilisant le fait que f est quand même de type pour a fixé sur les rationnels...

Je pense que c'est plus dans l'esprit des leçons du capes.

[lasaid]

khivapia
porriez vous m'expliquer le sens de normés dans ce théoréme
: "Soit linéaire de dans espaces vectoriels normés sur ou .

[khivapia]

Bonjour Lasaid

j'aurais plutôt dû le formuler comme "Soit E un -espace vectoriel normé, avec ou ".

c'est-à-dire un espace vectoriel de corps de base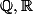 ou , muni d'une norme.

Une norme est une application || || : vérifiant les propriétés suivantes :


(inégalité triangulaire)

par exemple ici la norme considérée sur est la valeur absolue, selon laquelle la continuité "habituelle" est définie.

Grâce à une norme on peut définir une topologie sur les espaces (vectoriels notamment), c'est-à-dire des ouverts, des fermés, la notion de continuité etc. En particulier sur des espaces vectoriels on étudie spécialement la continuité des applications linéaires.


Pour en savoir plus, regarder un livre de topologie...

En espérant avoir un petit peu éclairci l'horizon

[lasaid]

merci beaucoup pour l'information