Equation de droite ds l'espace
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
jeje56
- Membre Irrationnel
- Messages: 1187
- Enregistré le: 16 Jan 2007, 20:10
-
 par jeje56 » 05 Mai 2007, 17:27
par jeje56 » 05 Mai 2007, 17:27
Dans R^3, est-il possible de déterminer l'équation d'une droite à partir de deux points de cette droite ?...
Merci
-
anima
- Membre Transcendant
- Messages: 3762
- Enregistré le: 15 Sep 2006, 11:00
-
 par anima » 05 Mai 2007, 17:33
par anima » 05 Mai 2007, 17:33
jeje56 a écrit:Dans R^3, est-il possible de déterminer l'équation d'une droite à partir de deux points de cette droite ?...
Merci
Si tu sous-entends dans l'espace "normal" (je ne suis pas ami avec les notations R^), alors oui. Enfin l'équation...un systeme d'équations d'une droite.
Tu trouves le vecteur directeur de la droite (AB, par exemple, si tes points sont A et B), et ensuite le systeme se présentera suivant la forme:
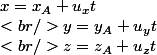
;\vec{u}(u_x,u_y,u_z))
Par contre, dans l'espace, il me semble qu'il est impossible d'avoir une équation cartésienne d'une droite.
(je peux me tromper, hein. C'est ce qu'on m'a appris en premiere :ptdr: )
-
jeje56
- Membre Irrationnel
- Messages: 1187
- Enregistré le: 16 Jan 2007, 20:10
-
 par jeje56 » 05 Mai 2007, 17:51
par jeje56 » 05 Mai 2007, 17:51
Qu'est ce que t ? Et d'où vient ton système?
Merci ;-)
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 05 Mai 2007, 18:00
par yos » 05 Mai 2007, 18:00
anima a écrit:Par contre, dans l'espace, il me semble qu'il est impossible d'avoir une équation cartésienne d'une droite.
(je peux me tromper, hein. C'est ce qu'on m'a appris en premiere :ptdr: )
En effet tout le monde peut se tromper.
x²+y²=0 c'est l'équation de quoi?
-
jeje56
- Membre Irrationnel
- Messages: 1187
- Enregistré le: 16 Jan 2007, 20:10
-
 par jeje56 » 05 Mai 2007, 18:19
par jeje56 » 05 Mai 2007, 18:19
Personne d'autre pr ma question ?...
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 05 Mai 2007, 18:38
par yos » 05 Mai 2007, 18:38
anima a tout dit. Le mieux est de représenter ta droite par un système d'équations paramétriques. t est le paramètre.
-
anima
- Membre Transcendant
- Messages: 3762
- Enregistré le: 15 Sep 2006, 11:00
-
 par anima » 05 Mai 2007, 18:57
par anima » 05 Mai 2007, 18:57
yos a écrit:En effet tout le monde peut se tromper.
x²+y²=0 c'est l'équation de quoi?
Bon ok. J'ai appris quelque chose aujourd'hui :zen:
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 05 Mai 2007, 20:12
par yos » 05 Mai 2007, 20:12
Exemple : la droite passant par A(3,8,4), dirigée par u(4,9,6) a pour représentation paramétrique (4t+3, 9t+8, 6t+4) . Ca veut dire que tu as là les coordonnées de tous les points de la droite en faisant varier t.
Avec t=0, tu retrouves le point A.
Avec t=12, tu as le point B(51, 116, 76)...
On peut pas faire plus simple et plus pratique.
-
jeje56
- Membre Irrationnel
- Messages: 1187
- Enregistré le: 16 Jan 2007, 20:10
-
 par jeje56 » 05 Mai 2007, 22:18
par jeje56 » 05 Mai 2007, 22:18
Dac, merci !
-
jeje56
- Membre Irrationnel
- Messages: 1187
- Enregistré le: 16 Jan 2007, 20:10
-
 par jeje56 » 05 Mai 2007, 22:21
par jeje56 » 05 Mai 2007, 22:21
Et sans paramètre, est ce possible? (système d'équations cartésiennes...)
 par taupeaveugle » 05 Mai 2007, 22:52
par taupeaveugle » 05 Mai 2007, 22:52
rappelle toi de ta lecon de 1er sur les barycentres de charges pondérées....
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 05 Mai 2007, 23:32
par fahr451 » 05 Mai 2007, 23:32
bonsoir
si tu élimines le paramètre t tu obtiendras un système de deux équations (linéaires) cartésiennes de la droite
chaque équation est l'équation d 'un plan
la droite étant l'intersection des deux plans.

-
nuage
- Membre Complexe
- Messages: 2214
- Enregistré le: 09 Fév 2006, 22:39
-
 par nuage » 05 Mai 2007, 23:50
par nuage » 05 Mai 2007, 23:50
Et après, si tu faire luxueux, tu peux imiter yos
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 06 Mai 2007, 07:56
par yos » 06 Mai 2007, 07:56
nuage a écrit:Et après, si tu faire luxueux, tu peux imiter yos
Qu'est-ce à dire?

-
nuage
- Membre Complexe
- Messages: 2214
- Enregistré le: 09 Fév 2006, 22:39
-
 par nuage » 06 Mai 2007, 22:40
par nuage » 06 Mai 2007, 22:40
Salut,
c'est à dire écrire :
^2+(a_2x+b_2y+c_2z+d_2)^2=0)
:ptdr:
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 07 Mai 2007, 00:17
par Flodelarab » 07 Mai 2007, 00:17
anima a écrit:Bon ok. J'ai appris quelque chose aujourd'hui :zen:
Alors là, moi aussi!
Je vais pouvoir aller me coucher moins ignorant.
Jolie façon de le dire :++:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 28 invités
