Bonjour, je dois résoudre l'équation différentielle (x^2 + 1)y' + 2xy =3x^2 + 1.
J'ai résolus l'équation homogène et je suis maintenant à la recherche d'une solution particulière. La correction me dit "on remarque que y0(x)= x convient". J'aimerais bien savoir comme je suis sensé le remarquer.
Merci d'avance !
Equation différentielle.
8 messages
- Page 1 sur 1
Re: Equation différentielle.
Bonsoir,
il y a une méthode, appelée variation de la constante, qui permet de trouver une solution particulière de l'équation.
La résolution de l'équation homogène donne
 où K est une constante d'intégration réelle.
où K est une constante d'intégration réelle.
Pour trouver une solution particulière, on pose
}{x^2+1}) (*)
(*)
on calcule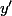
(x^2+1)-K(x).2x}{(x^2+1)^2})
En remplaçant y et y' dans l'équation, il vient:
=3x^2+1)
d'où
 où C est une constante d'intégration
où C est une constante d'intégration
avec (*) on obtient:

+ C}{x^2+1})
soit

conclusion: la méthode de variation de la constante a permis de trouver une solution particulière de l'équation.
il y a une méthode, appelée variation de la constante, qui permet de trouver une solution particulière de l'équation.
La résolution de l'équation homogène donne
Pour trouver une solution particulière, on pose
on calcule
En remplaçant y et y' dans l'équation, il vient:
d'où
avec (*) on obtient:
soit
conclusion: la méthode de variation de la constante a permis de trouver une solution particulière de l'équation.
Re: Equation différentielle.
mathelot a écrit:Bonsoir,
il y a une méthode, appelée variation de la constante, qui permet de trouver une solution particulière de l'équation.
La résolution de l'équation homogène donneoù K est une constante d'intégration réelle.
Pour trouver une solution particulière, on pose(*)
on calcule
En remplaçant y et y' dans l'équation, il vient:
d'oùoù C est une constante d'intégration
avec (*) on obtient:
soit
conclusion: la méthode de variation de la constante a permis de trouver une solution particulière de l'équation.
Merci, mais il peut y avoir plusieurs solutions particulière ?
Re: Equation différentielle.
oui, une infinité mais on s'en fiche, il faut en trouver au moins une.
Les solutions de l'équation sont de la forme:

L'ensemble des solutions est une droite affine.
Un point de cette droite est la fonction x.
Le vecteur directeur de cette droite est la fonction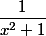
Comme toute droite affine, on peut choisir un autre point, par exemple:
+\dfrac{C}{x^2+1}) qui fournit une autre solution particulière.
qui fournit une autre solution particulière.
en fait, c'est tout bête, toute solution de l'équation peut être une solution particulière.
Les solutions de l'équation sont de la forme:
L'ensemble des solutions est une droite affine.
Un point de cette droite est la fonction x.
Le vecteur directeur de cette droite est la fonction
Comme toute droite affine, on peut choisir un autre point, par exemple:
en fait, c'est tout bête, toute solution de l'équation peut être une solution particulière.
Re: Equation différentielle.
mathelot a écrit:oui, une infinité mais on s'en fiche, il faut en trouver au moins une.
Les solutions de l'équation sont de la forme:
L'ensemble des solutions est une droite affine.
Un point de cette droite est la fonction x.
Le vecteur directeur de cette droite est la fonction
Comme toute droite affine, on peut choisir un autre point, par exemple:qui fournit une autre solution particulière.
en fait, c'est tout bête, toute solution de l'équation peut être une solution particulière.
Aaahh d'accord ! Merci beaucoup !
Re: Equation différentielle.
La méthode de variation de la constante est assez lourde.
On pouvait ici chercher une solution polynomiale, puisque les coefficients et le second membre sont des polynômes en .
.
Si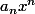 était le terme de plus haut degré d'une telle solution, le terme de plus haut degré du membre de gauche de l'équation serait
était le terme de plus haut degré d'une telle solution, le terme de plus haut degré du membre de gauche de l'équation serait a_nx^{n+1}) .
.
Je laisse continuer ...
On pouvait ici chercher une solution polynomiale, puisque les coefficients et le second membre sont des polynômes en
Si
Je laisse continuer ...
Re: Equation différentielle.
GaBuZoMeu a écrit:La méthode de variation de la constante est assez lourde.
On pouvait ici chercher une solution polynomiale, puisque les coefficients et le second membre sont des polynômes en.
Siétait le terme de plus haut degré d'une telle solution, le terme de plus haut degré du membre de gauche de l'équation serait
.
Je laisse continuer ...
Je te remercie, je pense réussir même sens la méthode de variation de la constante. Je savais juste pas qu'il pouvait y avoir une infinité de solutions particulière et comme la correction disais seulement "on remarque que x convient" je ne comprenais pas trop
Re: Equation différentielle.
Tu sais sans doute qu'une droite du plan est donnée par la droite vectorielle des vecteurs parallèles à cette droite et un point particulier de la droite. N'importe quel point de la droite peut servir de "point particulier".
Ici, c'est exactement la même histoire. Les solutions de l'équation homogène forment une droite vectorielle, et la droite affine des solutions de l'équation complète est donnée par cette droite vectorielle et une solution particulière de l'équation complète. Autrement dit, la solution générale de l'équation complète est la somme de la solution générale de l'équation homogène et d'une solution particulière de l'équation complète.
N'importe quelle solution de l'équation complète peut servir de "solution particulière", de même que n'importe quel point de la droite peut servir de point particulier.
Quand on recherche une solution particulière de l'équation complète, on peut imposer une condition ad hoc sur sa forme (comme, ici, d'être un polynôme) pour pouvoir calculer. De même, pour trouver un point sur une droite on peut en calculer l'intersection avec l'axe des ordonnées, par exemple.
Ici, c'est exactement la même histoire. Les solutions de l'équation homogène forment une droite vectorielle, et la droite affine des solutions de l'équation complète est donnée par cette droite vectorielle et une solution particulière de l'équation complète. Autrement dit, la solution générale de l'équation complète est la somme de la solution générale de l'équation homogène et d'une solution particulière de l'équation complète.
N'importe quelle solution de l'équation complète peut servir de "solution particulière", de même que n'importe quel point de la droite peut servir de point particulier.
Quand on recherche une solution particulière de l'équation complète, on peut imposer une condition ad hoc sur sa forme (comme, ici, d'être un polynôme) pour pouvoir calculer. De même, pour trouver un point sur une droite on peut en calculer l'intersection avec l'axe des ordonnées, par exemple.
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 33 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
