Bonjour,
dans cet exercice on me demande de montrer que l’équation différentielle (F) : 4U" + U^(2n+1) - U = 0 admet une solution unique, et ensuite déterminer cette solution. Sachant que dans la question précédente (la c'est bon il suffit de remplacer l'equation (F) par sa solution et on trouve que que Y est solution de (E)) on me demande de montrer : Y est solution de l’équation (E) définit par (E) Y" + Y^(2n+1)/(4x^(n+2))=0 <==> U(t)=Y(exp(t))exp(-t/2) est est solution de (F).
je pense qu il faut trouver la solution de l’équation (E) et remplacer Y dans U . Mais je n'arrive pas à l’intégrer.
N.B:( Y et U sont de classe C^2)
Merci d'avance.
équation différentielle 4U" + U^(2n+1) - U = 0
4 messages
- Page 1 sur 1
Re: équation différentielle 4U" + U^(2n+1) - U = 0
les fonctions 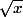 et
et  sont solutions de (E)
sont solutions de (E)
je n'en sais pas plus .
je n'en sais pas plus .
Re: équation différentielle 4U" + U^(2n+1) - U = 0
tournesol a écrit:les fonctionset
sont solutions de (E)
je n'en sais pas plus .
Comment t a obtenu ce resultat
Re: équation différentielle 4U" + U^(2n+1) - U = 0
2n+1 étant impair , j'ai remarqué que Y solution de (E) ssi - Y solution de (E) .
D'autre part compte tenu de la présence d'exposants dans l'équation , j'ai recherché une solution du type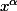 et j'ai trouvé
et j'ai trouvé 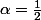
D'autre part compte tenu de la présence d'exposants dans l'équation , j'ai recherché une solution du type
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 47 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
