équation différentielle

[nix64]

Bonjour

pourquoi il n a pas fait la preuve comme ça il a dit que c est une preuve rapide et pas rigoureuse pourquoi on a pas fait comme ça

[LB2]

En fait, ton idée est bonne est convient "en pratique" pour intégrer la plupart des équations différentielles qu'on appelle à variables séparables.

Le souci ici c'est que tu confonds allégrement "y n'est pas la fonction nulle" et "y ne s'annule jamais".

En fait, un théorème puissant nous dit que si "y n'est pas la fonction nulle", alors "y ne s'annule jamais" (Cauchy Lipschitz) mais c'est pas du tout trivial.

[nix64]

oui j ai vraiment confondu en tre la fonction nulle et ne s annule jamais merci
a propos du th de Cauchy Lipschitz
y: x ->x-2 n est pas la fonction nulle mais elle s annule en 2

[LB2]

oui mais y:x->x-2 n'est pas solution de ton équa diff.

Tu remarques qu'ici les exponentielles ne s'annulent pas sur R

[mathelot]

bjr,
pour que le problème soit bien posé, il faut une condition initiale:

Soit un intervalle ouvert contenant

supposons
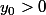
Dans un voisinage connexe V de , y reste strictement positive , par continuité.
On peut donc écrire

On intégre de à

soit

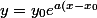On vérifie ensuite que est la solution maximale du système.
On fait de même dans le cas

[nix64]

s il vous plait dans la preuve du théorème 1 pourquoi cette fonction z d ou vient cette fonction z ?

[mathelot]

on veut montrer que les solutions sont de la forme

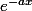
en multiplant par des deux côtés , on doit montrer que
est une fonction constante.