Bonjour,
J'ai l'équation différentielle suivante à résoudre sur ]0,+infini[ : x²y''+xy'+y=0.
La première question de mon exercice est la suivante : En posant x=exp(u), déterminer une équation différentielle satisfaite par y en u.
Je ne comprends pas cette question. J'essaie de trouver une équation en y(u), mais je ne m'en sors pas....
Merci de votre aide.
Bonne fin de journée.
équation différentielle
10 messages
- Page 1 sur 1
D'accord, j'ai bien compris la réponse de chan79.
J'avais totalement oublié la formule reprécisée par vingtdieux.
Merci à vous deux.
Par contre, même si je comprends vos raisonnements, j'ai du mal à comprendre pourquoi nous avons bien répondu à la question "déterminer une équation différentielle satisfaite par y en u".
Pour moi, il fallait trouver une équation en y(u), alors que l'équation proposée par chan79 est en z(u)....
J'avais totalement oublié la formule reprécisée par vingtdieux.
Merci à vous deux.
Par contre, même si je comprends vos raisonnements, j'ai du mal à comprendre pourquoi nous avons bien répondu à la question "déterminer une équation différentielle satisfaite par y en u".
Pour moi, il fallait trouver une équation en y(u), alors que l'équation proposée par chan79 est en z(u)....
Je vais peut-être dire des conneries (ça sera pas la première... ni la dernière... :zen: ), mais a mon avis, tout dépend des notations que l'on utilise :
- Pour un "pur matheux", il faut faire comme chan79 l'a fait, c'est à dire donner un nouveau nom (à savoir z) à la fonction y(ln(x)) et la nouvelle équation différentielle qu'on cherche est évidement une équation en z.
- Du point de vue "plus physicien", il me semble (je suis nul en physique) qu'on peut garder la même lettre qui représente la même "quantité observable", mais que par contre, on n'écrit jamais de y' ou de y'', mais des dy/dx ou des d²y/dx² qui précisent à la fois la fonction qu'on dérive, mais aussi la variable par rapport à laquelle on dérive.
Donc un physicien, risque de remplacer le y' et le z' de chan79 respectivement par dy/dx et dy/du
Perso (je suis matheux), j'ai un peu du mal avec les notation physicienne, donc en particulier avec un truc comme ce qu'a écrit vingtdieux quelque post çi dessus, mais je reconnais que, très souvent, leur notation permet d'écrire les chose de façon plus concise qu'en math : par exemple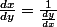 semble plus "naturel" que
semble plus "naturel" que '=\frac{1}{f'\circ f^{-1}}) (mais moi, j'ai souvent du mal à y retrouver "mes petits"...
(mais moi, j'ai souvent du mal à y retrouver "mes petits"...  )
)
Bilan : à toi de voir ce que tu préfère (et surtout à ne pas trop t'emmêler les pinceaux entre les deux...)
- Pour un "pur matheux", il faut faire comme chan79 l'a fait, c'est à dire donner un nouveau nom (à savoir z) à la fonction y(ln(x)) et la nouvelle équation différentielle qu'on cherche est évidement une équation en z.
- Du point de vue "plus physicien", il me semble (je suis nul en physique) qu'on peut garder la même lettre qui représente la même "quantité observable", mais que par contre, on n'écrit jamais de y' ou de y'', mais des dy/dx ou des d²y/dx² qui précisent à la fois la fonction qu'on dérive, mais aussi la variable par rapport à laquelle on dérive.
Donc un physicien, risque de remplacer le y' et le z' de chan79 respectivement par dy/dx et dy/du
Perso (je suis matheux), j'ai un peu du mal avec les notation physicienne, donc en particulier avec un truc comme ce qu'a écrit vingtdieux quelque post çi dessus, mais je reconnais que, très souvent, leur notation permet d'écrire les chose de façon plus concise qu'en math : par exemple
Bilan : à toi de voir ce que tu préfère (et surtout à ne pas trop t'emmêler les pinceaux entre les deux...)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
x²y''+xy'+y=0
x = e^u
dx = e^u du
du/dx = e^-u
dy/dx = dy/du * (du/dx)
dy/dx = dy/du * (du/dx) = dy/du * e^-u
d²y/dx² = d(dy/dx)/dx = d(dy/du * e^-u)/dx
d²y/dx² = d(dy/du * e^-u)/du * du/dx
d²y/dx² = (d²y/du² * e^-u - e^-u * dy/du)* e^-u
d²y/dx² = e^(-2u) * (d²y/du² - dy/du)
e^(2u) * e^(-2u) * (d²y/du² - dy/du) + e^u * dy/du * e^-u + y = 0
d²y/du² - dy/du + dy/du + y = 0
d²y/du² + y = 0
y = A.cos(u) + B.sin(u)
y = A.cos(ln|x|) + B.sin(ln|x|)
:zen:
x = e^u
dx = e^u du
du/dx = e^-u
dy/dx = dy/du * (du/dx)
dy/dx = dy/du * (du/dx) = dy/du * e^-u
d²y/dx² = d(dy/dx)/dx = d(dy/du * e^-u)/dx
d²y/dx² = d(dy/du * e^-u)/du * du/dx
d²y/dx² = (d²y/du² * e^-u - e^-u * dy/du)* e^-u
d²y/dx² = e^(-2u) * (d²y/du² - dy/du)
e^(2u) * e^(-2u) * (d²y/du² - dy/du) + e^u * dy/du * e^-u + y = 0
d²y/du² - dy/du + dy/du + y = 0
d²y/du² + y = 0
y = A.cos(u) + B.sin(u)
y = A.cos(ln|x|) + B.sin(ln|x|)
:zen:
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 31 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
