Equation différentielle du premier ordre
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
ordage
- Membre Naturel
- Messages: 13
- Enregistré le: 12 Déc 2017, 10:15
-
 par ordage » 27 Aoû 2018, 18:40
par ordage » 27 Aoû 2018, 18:40
Bonjour
Dans un problème de physique , je dois tracer une courbe plane en coordonnées polaires qui répond à l'équation suivante:
^2 = -( r(\varphi))^2 + \frac{(5+4 \cos(\varphi))^2}{(1 + 0.5 \cos\varphi)^4})
une telle equation a-t-elle une solution analytique?
Je n'en ai pas trouvé.
J'ai fait une résolution numérique qu me laisse perplexe ( avec rk de wsMaxima 14.12.1) peut-on faire confiance à ce logiciel?
Merci pour toute info utile.
Cordialement.
-
aviateur
 par aviateur » 28 Aoû 2018, 16:09
par aviateur » 28 Aoû 2018, 16:09
Bonjour
C'est quoi ton problème de physique?
Tel quel, je ne vois pas comment numériquement tu peux calculer une solution puisque il manque une condition (condition initiale par exemple).
Ensuite trouver une solution générale analytiquement me semble à première vue un peu difficile mais peut être pas impossible.
Mais avant toute recherche sur une réponse possible, je me demande si il n'y a pas une erreur
c'est à dire au numérateur tu n'aurais pas
)
à la place de
^2)
par hasard??
-
ordage
- Membre Naturel
- Messages: 13
- Enregistré le: 12 Déc 2017, 10:15
-
 par ordage » 28 Aoû 2018, 17:25
par ordage » 28 Aoû 2018, 17:25
Bonjour
Merci pour ta réponse
L'équation est correcte. On peut définir des conditions intiales pour
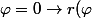 = 4, \frac{dr(\varphi)}{d \varphi} =0)
Le problème se rencontre à propos de la physique (orbites autour du soleil) , mais c'est problème géométrique.
C'est la représentation isométrique (même paramètre affine ) d'une courbe (dans un espace à deux dimensions) définie dans un espace non euclidien (en fait conformément euclidien qui a donc une courbure non nulle) dans un espace euclidien (pour représenter le phénomène lié au paramètre affine sur un graphe plan en géométrie euclidienne) qui conduit à cette équation.
Cela parait tordu, mais cela résulte d'une proposition géométrique de Painlevé en 1921 pour décrire ce mouvement (Painlevé qui en plus de la politique faisait aussi des mathématiques à ses heures perdues).
Cordialement
-
aviateur
 par aviateur » 28 Aoû 2018, 17:52
par aviateur » 28 Aoû 2018, 17:52
Parce que justement s'il n'y avait pas de carré (comme je te l'ai dit) alors la solution est facile et cela correspond à une orbite elliptique.
Maintenant tes conditions initiales sont cohérentes avec ton équation.
La résolution numérique comme ça sans analyse plus approfondie va poser des problèmes. En effet il ya encore une indéterminée dans ton équation c'est le signe de r'. En effet r' intervient au carré.
Donc cela dépend encore de ton problème physique.
Maintenant j'ai donné ça à manger à un logiciel (donc par définition je ne gère pas la résolution) et il me donne une solution pour des valeurs t assez petit (<t=1.3) . La courbe est une sorte de spirale qui va en grandissant.
C'est à dire on est parti sur du r'>0. Et c'est logique que la machine soit perdue. Car ta solution explose.
Or r'>0 , r augmente et r'^2+r^2= une fonction de t qui est borné.
Tu as un temps limite.
Mais ce n'est pas la peine d'aller + loin pour moi car c'est peut être l'autre cas (r'<0) qu'il faut prendre et tout dépend du problème physique.
Quant à une solution analytique ds un ou l'autre cas. Je n'ai pas de réponse pour l'instant.
-
ordage
- Membre Naturel
- Messages: 13
- Enregistré le: 12 Déc 2017, 10:15
-
 par ordage » 31 Aoû 2018, 14:40
par ordage » 31 Aoû 2018, 14:40
Bonjour
Effectivement, lorsqu'on intègre numériquement de -pi à + pi , on doit changer le signe de la racine donnant le signe de la dérivée 4 fois ( +, -, +, -), aux points où la dérivée s'annule (elle s'annule 4 fois).
La courbe est l'assemblage de 4 morceaux qui se raccordent. Difficile de faire cette intégration numérique avec un progiciel (où on n'a pas accès au code) car il faudrait insérer des tests de nullité de la dérivée pour changer le signe de la dérivée.
Cordialement
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 63 invités
