Équation différentielle d'ordre 1

[Sheigh]

Bonjour à tous,

Je souhaite résoudre par la méthode de la variation de la constante l'équation différentielle suivante :
(1+x) y'+y = 1+ ln (1+x) sur ]-1;+infini[
j'ai commencé par résoudre l'équation homogène, jusque là ça va : y=A/(1+x)
Puis la solution particulière par variation de la constante, j'ai commencé comme ceci:
y =A/(1+x)
y' = A'/(1+x) - A /(1+x)^2
...
A'=1+ln(1+x)
donc pour trouver A je me retrouve bloquée car je pensais donner comme primitive x + primitive de ln(1+x) mais pour ln (1+x) je me plonge dans une intégration par partie mais sans succès. Pouvez-vous m'éclairer pour trouver A.
Je vous remercie par avance.

[aviateur]

Bonjour pour le log:

Cette dernière primitive étant facile à calculer
Mais attention aux détails de la résolution de l'équadif...

[Sheigh]

Sur mon brouillon j'arrive à ce même même résulat:

Lorsque je continue j'ai : x*ln(1+x)-ln(1+x)/x ....> ( x^2*ln(1+x)-ln(1+x))/x là je ne suis pas convaincue, alors que oui ça semble simple !

Que voulez-vous dire par les détails de la résolutions de l'équadiff ?

[aviateur]

Je n'arrive pas à lire la suite de
"Lorsque je continue j'ai..... "

Que voulez-vous dire par les détails de la résolutions de l'équadiff ?
Je retire cette remarque, je n'avais pas vu que le domaine de définition était donné.

[Sheigh]

Alors comme résultat j'avis ceci :
(x^2*ln(1+x)-ln(1+x))/x

[aviateur]

Franchement je ne comprends toujours pas. "Comme résultat j'ai" : mais résultat de quoi?
Du calcul de la primitive de \ln(1+x)? où de l'équation différentielle?
Comment calcules tu ? Le problème est-il là?

Ensuite la variation de la constante on pouvait sans passer mais là c'est un autre problème.

[aviateur]

Je viens de comprendre: non ce n'est pas cela
On a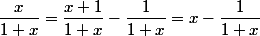
c'est cela qu'il faut faire.

[Sheigh]

D'accord, merci, je vois mieux
On a
c'est cela qu'il faut faire.

si j'ai bien compris, il faut ajouter et retirer 1 à x et ainsi intégrer, c'est quelque chose que je ne pensais pas du tout, j'ai pu ainsi continuer avec vos indications et trouver la solution générale de l'équation.